3D general plotting

NOTE: For technical reasons, all interactive-widgets plots in this documentation are created using Holoviz’s Panel. Often, they will ran just fine with ipywidgets too. However, if a specific example uses the param library, or widgets from the panel module, then users will have to modify the params dictionary in order to make it work with ipywidgets. Refer to Interactive module for more information.

spb.graphics.functions_3d.line_parametric_3d(expr1, expr2, expr3, range=None, label=None, rendering_kw=None, colorbar=True, use_cm=True, **kwargs)

Plots a 3D parametric curve.

Parameters:

expr1, expr2, expr3Expr or callable

The expression representing x component of the parametric function. It can be a:

• Symbolic expression representing the function of one variable to be plotted.

• Numerical function of one variable, supporting vectorization. In this case the following keyword arguments are not supported: params.

range(symbol, min, max)

A 3-tuple denoting the range of the parameter variable.

labelstr, optional

An optional string denoting the label of the expression to be visualized on the legend. If not provided, the string representation of the expression will be used.

rendering_kwdict, optional

A dictionary of keywords/values which is passed to the backend’s function to customize the appearance of lines. Refer to the plotting library (backend) manual for more informations.

adaptivebool, optional

Setting adaptive=True activates the adaptive algorithm implemented in [python-adaptive] to create smooth plots. Use adaptive_goal and loss_fn to further customize the output.

The default value is False, which uses an uniform sampling strategy, where the number of discretization points is specified by the n keyword argument.

adaptive_goalcallable, int, float or None

Controls the “smoothness” of the evaluation. Possible values:

• None (default): it will use the following goal: lambda l: l.loss() < 0.01

• number (int or float). The lower the number, the more evaluation points. This number will be used in the following goal: lambda l: l.loss() < number

• callable: a function requiring one input element, the learner. It must return a float number. Refer to [python-adaptive] for more information.

colorbarboolean, optional

Show/hide the colorbar. Default to True (colorbar is visible). Only works when use_cm=True.

color_funccallable, optional

Define the line color mapping when use_cm=True. It can either be:

• A numerical function supporting vectorization. The arity can be:

  • 1 argument: f(t), where t is the parameter.

  • 3 arguments: f(x, y, z) where x, y, z are the coordinates of the points.

  • 4 arguments: f(x, y, z, t).

• A symbolic expression having at most as many free symbols as expr_x or expr_y or expr_z.

• None: the default value (color mapping applied to the parameter).

force_real_evalboolean, optional

Default to False, with which the numerical evaluation is attempted over a complex domain, which is slower but produces correct results. Set this to True if performance is of paramount importance, but be aware that it might produce wrong results. It only works with adaptive=False.

scatterboolean, optional

Default to False, which will render a line connecting all the points. If True, a scatter plot will be generated.

loss_fncallable or None

The loss function to be used by the adaptive learner. Possible values:

• None (default): it will use the default_loss from the adaptive module.

• callable : Refer to [python-adaptive] for more information. Specifically, look at adaptive.learner.learner1D to find more loss functions.

nint, optional

Used when the adaptive=False. The function is uniformly sampled at n number of points. Default value to 1000. If the adaptive=True, this parameter will be ignored.

paramsdict

A dictionary mapping symbols to parameters. This keyword argument enables the interactive-widgets plot, which doesn’t support the adaptive algorithm (meaning it will use adaptive=False). Learn more by reading the documentation of the interactive sub-module.

tx, ty, tz, tpcallable, optional

Apply a numerical function to the x, y, z directions and to the discretized parameter.

use_cmboolean, optional

If True, apply a color map to the parametric lines. If False, solid colors will be used instead. Default to True.

xscale‘linear’ or ‘log’, optional

Sets the scaling of the parameter.

Returns:

serieslist

A list containing one instance of Parametric3DLineSeries.

See also

spb.graphics.functions_2d.line_parametric_2d, list_3d

Examples

>>> from sympy import symbols, cos, sin, pi, root
>>> from spb import *
>>> t = symbols('t')

(Source code)

Single plot.

>>> graphics(line_parametric_3d(cos(t), sin(t), t, (t, -5, 5)))
Plot object containing:
[0]: 3D parametric cartesian line: (cos(t), sin(t), t) for t over (-5.0, 5.0)

(Source code, png)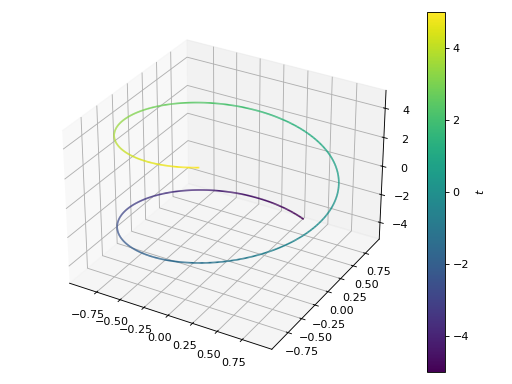

Customize the appearance by setting a label to the colorbar, changing the colormap and the line width.

>>> graphics(
...     line_parametric_3d(
...         3 * sin(t) + 2 * sin(3 * t), cos(t) - 2 * cos(3 * t), cos(5 * t),
...         (t, 0, 2 * pi), "t [rad]", {"cmap": "hsv", "lw": 1.5}
...     )
... )
Plot object containing:
[0]: 3D parametric cartesian line: (3*sin(t) + 2*sin(3*t), cos(t) - 2*cos(3*t), cos(5*t)) for t over (0.0, 6.283185307179586)

(Source code, png)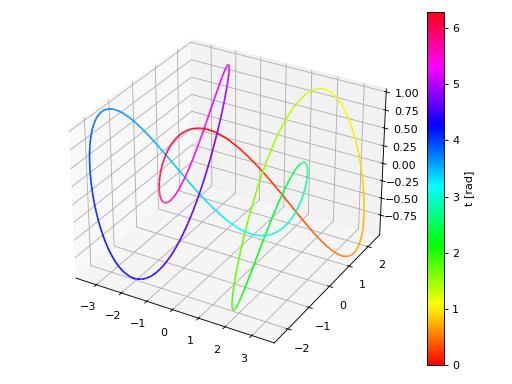

Plot multiple parametric 3D lines with different ranges:

>>> a, b, n = 2, 1, 4
>>> p, r, s = symbols("p r s")
>>> xp = a * cos(p) * cos(n * p)
>>> yp = a * sin(p) * cos(n * p)
>>> zp = b * cos(n * p)**2 + pi
>>> xr = root(r, 3) * cos(r)
>>> yr = root(r, 3) * sin(r)
>>> zr = 0
>>> graphics(
...     line_parametric_3d(
...         xp, yp, zp, (p, 0, pi if n % 2 == 1 else 2 * pi), "petals",
...         use_cm=False),
...     line_parametric_3d(xr, yr, zr, (r, 0, 6*pi), "roots",
...         use_cm=False),
...     line_parametric_3d(-sin(s)/3, 0, s, (s, 0, pi), "stem",
...         use_cm=False)
... )
Plot object containing:
[0]: 3D parametric cartesian line: (2*cos(p)*cos(4*p), 2*sin(p)*cos(4*p), cos(4*p)**2 + pi) for p over (0.0, 6.283185307179586)
[1]: 3D parametric cartesian line: (r**(1/3)*cos(r), r**(1/3)*sin(r), 0) for r over (0.0, 18.84955592153876)
[2]: 3D parametric cartesian line: (-sin(s)/3, 0, s) for s over (0.0, 3.141592653589793)

(Source code, png)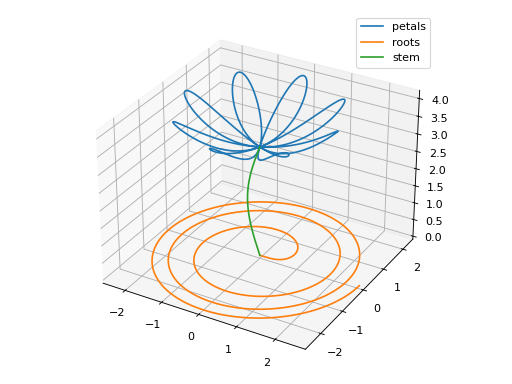

Plotting a numerical function instead of a symbolic expression, using Plotly:

from spb import *
import numpy as np
fx = lambda t: (1 + 0.25 * np.cos(75 * t)) * np.cos(t)
fy = lambda t: (1 + 0.25 * np.cos(75 * t)) * np.sin(t)
fz = lambda t: t + 2 * np.sin(75 * t)
graphics(
    line_parametric_3d(fx, fy, fz, ("t", 0, 6 * np.pi),
        rendering_kw={"line": {"colorscale": "bluered"}},
        adaptive=False, n=1e04),
    title="Helical Toroid", backend=PB)

(Source code, png)

Interactive-widget plot of the parametric line over a tennis ball. Refer to the interactive sub-module documentation to learn more about the params dictionary. This plot illustrates:

• combining together different plots.

• the use of prange (parametric plotting range).

• the use of the params dictionary to specify sliders in their basic form: (default, min, max).

from sympy import *
from spb import *
import k3d
a, b, s, e, t = symbols("a, b, s, e, t")
c = 2 * sqrt(a * b)
r = a + b
params = {
    a: (1.5, 0, 2),
    b: (1, 0, 2),
    s: (0, 0, 2),
    e: (2, 0, 2)
}
graphics(
    surface_revolution(
        (r * cos(t), r * sin(t)), (t, 0, pi),
        params=params, n=50, parallel_axis="x", show_curve=False,
        rendering_kw={"color":0x353535},
        force_real_eval=True
    ),
    line_parametric_3d(
        a * cos(t) + b * cos(3 * t),
        a * sin(t) - b * sin(3 * t),
        c * sin(2 * t), prange(t, s*pi, e*pi),
        rendering_kw={"color_map": k3d.matplotlib_color_maps.Summer},
        params=params
    ),
    backend=KB
)

(Source code, small.png)

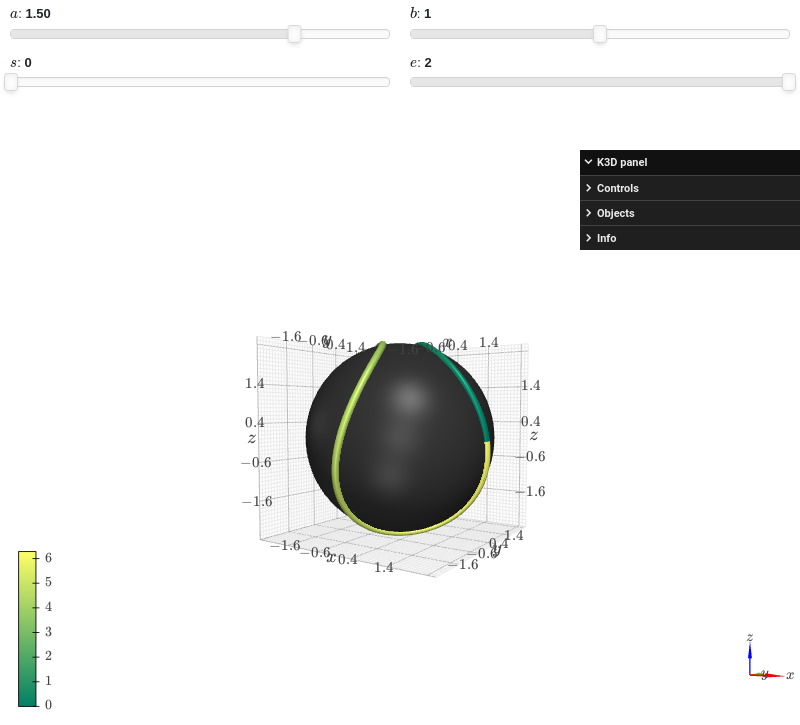
spb.graphics.functions_3d.list_3d(coord_x, coord_y, coord_z, label=None, rendering_kw=None, **kwargs)

Plots lists of coordinates in 3D space.

Parameters:

coord_x, coord_y, coord_zlist or tuple or 1D NumPy array

Lists of coordinates.

labelstr, optional

The label to be shown in the legend.

rendering_kwdict, optional

A dictionary of keywords/values which is passed to the backend’s function to customize the appearance of lines. Refer to the plotting library (backend) manual for more informations.

color_funccallable, optional

A numerical function of 3 variables, x, y, z defining the line color. Default to None. Requires use_cm=True in order to be applied.

scatterboolean, optional

Default to False, which will render a line connecting all the points. If True, a scatter plot will be generated.

fillboolean, optional

Default to True, which will render filled circular markers. It only works if scatter=True. If True, filled circular markers will be rendered. Note that some backend might not support this feature.

paramsdict

A dictionary mapping symbols to parameters. This keyword argument enables the interactive-widgets plot. Learn more by reading the documentation of the interactive sub-module.

use_cmboolean, optional

If True, apply a color map to the parametric lines. If False, solid colors will be used instead. Default to True.

Returns:

serieslist

A list containing one instance of List3DSeries.

See also

spb.graphics.functions_2d.line, line_parametric_3d

Examples

>>> from sympy import *
>>> from spb import *
>>> import numpy as np

(Source code)

Plot the coordinates of a single function:

>>> z = np.linspace(0, 6*np.pi, 100)
>>> x = z * np.cos(z)
>>> y = z * np.sin(z)
>>> graphics(list_3d(x, y, z))
Plot object containing:
[0]: 3D list plot

(Source code, png)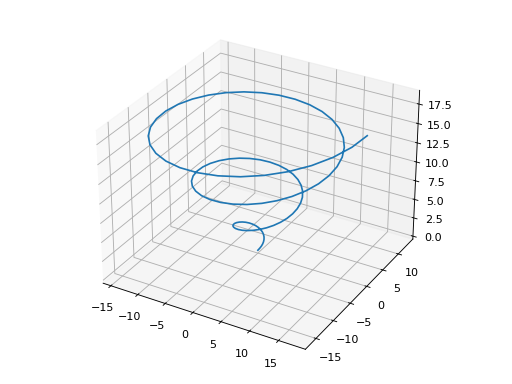

Plotting multiple functions with custom rendering keywords:

>>> graphics(
...     list_3d(x, y, z, "A"),
...     list_3d(x, y, -z, "B", {"linestyle": "--"}))
Plot object containing:
[0]: 3D list plot
[1]: 3D list plot

(Source code, png)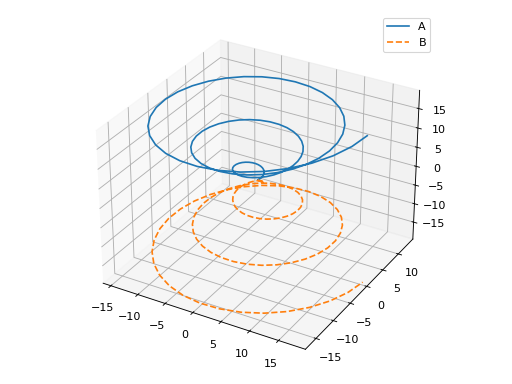

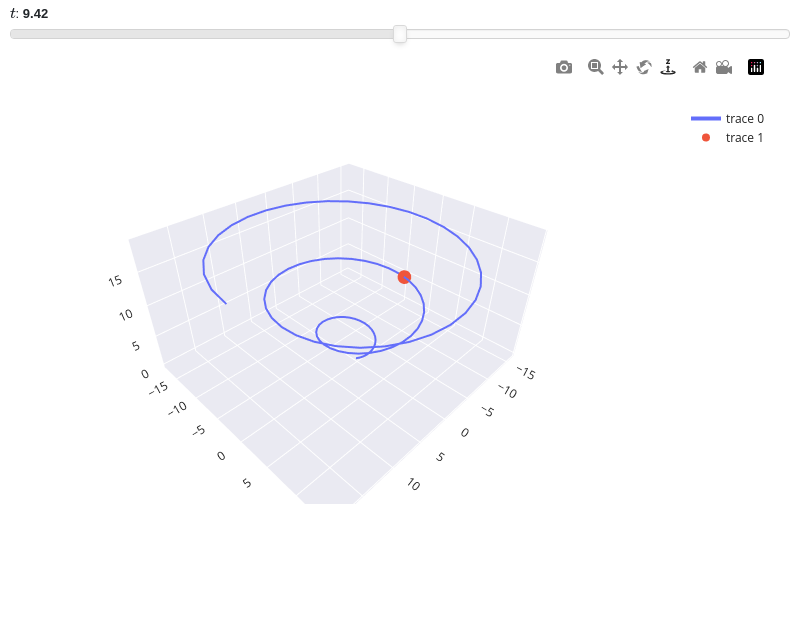
Interactive-widget plot of a dot following a path. Refer to the interactive sub-module documentation to learn more about the params dictionary.

from sympy import *
from spb import *
import numpy as np
t = symbols("t")
z = np.linspace(0, 6*np.pi, 100)
x = z * np.cos(z)
y = z * np.sin(z)
graphics(
    list_3d(x, y, z, scatter=False),
    list_3d(t * cos(t), t * sin(t), t,
        params={t: (3*pi, 0, 6*pi)}, scatter=True),
    backend=PB
)

(Source code, small.png)

spb.graphics.functions_3d.surface(expr, range1=None, range2=None, label=None, rendering_kw=None, colorbar=True, use_cm=False, **kwargs)

Creates the surface of a function of 2 variables.

Parameters:

exprExpr or callable

Expression representing the function of two variables to be plotted. The expression representing the function of two variables to be plotted. It can be a:

• Symbolic expression.

• Numerical function of two variable, supporting vectorization. In this case the following keyword arguments are not supported: params.

range1, range2: (symbol, min, max)

A 3-tuple denoting the range of the first and second variable, respectively. Default values: min=-10 and max=10.

labelstr, optional

The label to be shown in the colorbar. If not provided, the string representation of expr will be used.

rendering_kwdict, optional

A dictionary of keywords/values which is passed to the backend’s function to customize the appearance of surfaces. Refer to the plotting library (backend) manual for more informations.

adaptivebool, optional

The default value is set to False, which uses a uniform sampling strategy with number of discretization points n1 and n2 along the x and y directions, respectively.

Set adaptive to True to use the adaptive algorithm implemented in [python-adaptive] to create smooth plots. Use adaptive_goal and loss_fn to further customize the output.

adaptive_goalcallable, int, float or None

Controls the “smoothness” of the evaluation. Possible values:

• None (default): it will use the following goal: lambda l: l.loss() < 0.01

• number (int or float). The lower the number, the more evaluation points. This number will be used in the following goal: lambda l: l.loss() < number

• callable: a function requiring one input element, the learner. It must return a float number. Refer to [python-adaptive] for more information.

colorbarboolean, optional

Show/hide the colorbar. Default to True (colorbar is visible). Only works when use_cm=True.

color_funccallable, optional

Define the surface color mapping when use_cm=True. It can either be:

• A numerical function of 3 variables, x, y, z (the points computed by the internal algorithm) supporting vectorization.

• A symbolic expression having at most as many free symbols as expr.

• None: the default value (color mapping applied to the z-value of the surface).

force_real_evalboolean, optional

Default to False, with which the numerical evaluation is attempted over a complex domain, which is slower but produces correct results. Set this to True if performance is of paramount importance, but be aware that it might produce wrong results. It only works with adaptive=False.

is_polarboolean, optional

Default to False. If True, requests a polar discretization. In this case, range1 represents the radius, range2 represents the angle.

loss_fncallable or None

The loss function to be used by the adaptive learner. Possible values:

• None (default): it will use the default_loss from the adaptive module.

• callable : Refer to [python-adaptive] for more information. Specifically, look at adaptive.learner.learnerND to find more loss functions.

n, n1, n2int, optional

Number of discretization points along the two ranges. Default to 100. n is a shortcut to set the same number of discretization points on both directions.

paramsdict

A dictionary mapping symbols to parameters. This keyword argument enables the interactive-widgets plot, which doesn’t support the adaptive algorithm (meaning it will use adaptive=False). Learn more by reading the documentation of the interactive sub-module.

tx, ty, tzcallable, optional

Apply a numerical function to the discretized domain in the x, y and z direction, respectively.

use_cmboolean, optional

If True, apply a color map to the surface. If False, solid colors will be used instead. Default to False.

wireframeboolean, optional

Enable or disable a wireframe over the surface. Depending on the number of wireframe lines (see wf_n1 and wf_n2), activating this option might add a considerable overhead during the plot’s creation. Default to False (disabled).

wf_n1, wf_n2int, optional

Number of wireframe lines along the two ranges, respectively. Default to 10. Note that increasing this number might considerably slow down the plot’s creation.

wf_npointsint or None, optional

Number of discretization points for the wireframe lines. Default to None, meaning that each wireframe line will have n1 or n2 number of points, depending on the line direction.

wf_rendering_kwdict, optional

A dictionary of keywords/values which is passed to the backend’s function to customize the appearance of wireframe lines.

xscale, yscale‘linear’ or ‘log’, optional

Sets the scaling of the discretized ranges.

Returns:

serieslist

A list containing one instance of SurfaceOver2DRangeSeries and possibly multiple instances of Parametric3DLineSeries, if wireframe=True.

See also

spb.graphics.functions_2d.contour, surface_parametric, surface_spherical

surface_revolution, wireframe, plane

Examples

>>> from sympy import symbols, cos, sin, pi, exp
>>> from spb import *
>>> x, y = symbols('x y')

(Source code)

Single plot with Matplotlib:

>>> graphics(surface(cos((x**2 + y**2)), (x, -3, 3), (y, -3, 3)))
Plot object containing:
[0]: cartesian surface: cos(x**2 + y**2) for x over (-3.0, 3.0) and y over (-3.0, 3.0)

(Source code, png)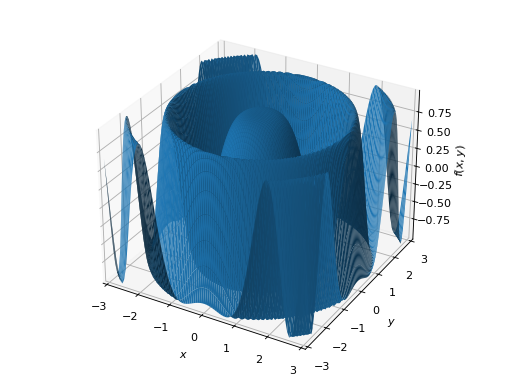

Single plot with Plotly, illustrating how to apply:

• a color map: by default, it will map colors to the z values.

• wireframe lines to better understand the discretization and curvature.

• transformation to the discretized ranges in order to convert radians to degrees.

• custom aspect ratio with Plotly.

from sympy import symbols, sin, cos, pi
from spb import *
import numpy as np
x, y = symbols("x, y")
expr = (cos(x) + sin(x) * sin(y) - sin(x) * cos(y))**2
graphics(
    surface(expr, (x, 0, pi), (y, 0, 2 * pi), use_cm=True,
        tx=np.rad2deg, ty=np.rad2deg,
        wireframe=True, wf_n1=20, wf_n2=20),
    backend=PB, xlabel="x [deg]", ylabel="y [deg]",
    aspect=dict(x=1.5, y=1.5, z=0.5))

(Source code, png)

Multiple plots with same range using color maps. By default, colors are mapped to the z values:

>>> graphics(
...     surface(x*y, (x, -5, 5), (y, -5, 5), use_cm=True),
...     surface(-x*y, (x, -5, 5), (y, -5, 5), use_cm=True))
Plot object containing:
[0]: cartesian surface: x*y for x over (-5.0, 5.0) and y over (-5.0, 5.0)
[1]: cartesian surface: -x*y for x over (-5.0, 5.0) and y over (-5.0, 5.0)

(Source code, png)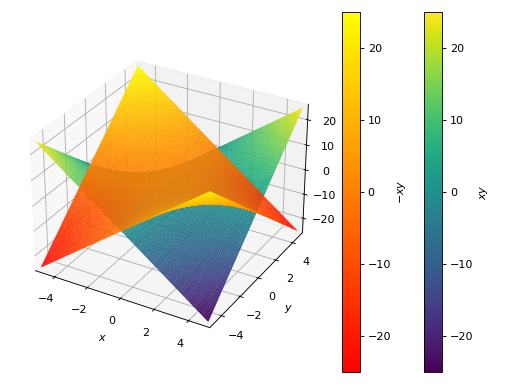

Multiple plots with different ranges and solid colors.

>>> f = x**2 + y**2
>>> graphics(
...     surface(f, (x, -3, 3), (y, -3, 3)),
...     surface(-f, (x, -5, 5), (y, -5, 5)))
Plot object containing:
[0]: cartesian surface: x**2 + y**2 for x over (-3.0, 3.0) and y over (-3.0, 3.0)
[1]: cartesian surface: -x**2 - y**2 for x over (-5.0, 5.0) and y over (-5.0, 5.0)

(Source code, png)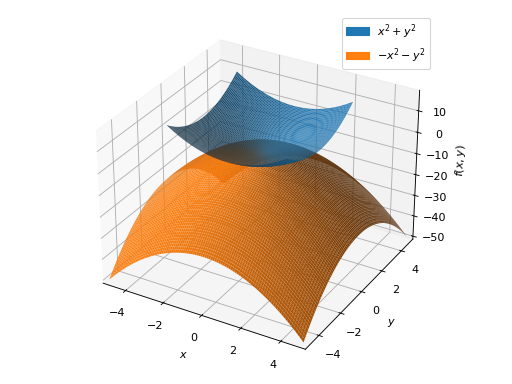

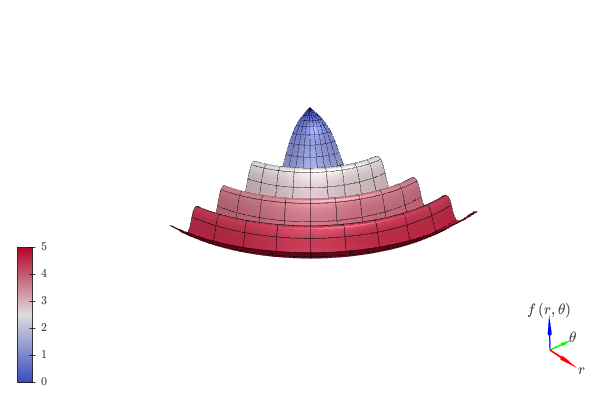
Single plot with a polar discretization, a color function mapping a colormap to the radius. Note that the same result can be achieved with plot3d_revolution.

from sympy import *
from spb import *
import numpy as np
r, theta = symbols("r, theta")
expr = cos(r**2) * exp(-r / 3)
graphics(
    surface(expr, (r, 0, 5), (theta, 1.6 * pi, 2 * pi),
        use_cm=True, color_func=lambda x, y, z: np.sqrt(x**2 + y**2),
        is_polar=True,
        wireframe=True, wf_n1=30, wf_n2=10,
        wf_rendering_kw={"width": 0.005}),
    backend=KB, legend=True, grid=False)

(Source code, small.png)

Plotting a numerical function instead of a symbolic expression:

>>> graphics(
...     surface(lambda x, y: x * np.exp(-x**2 - y**2),
...         ("x", -3, 3), ("y", -3, 3), use_cm=True))  

(Source code, png)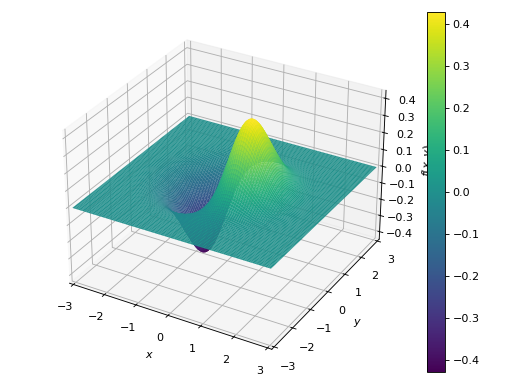

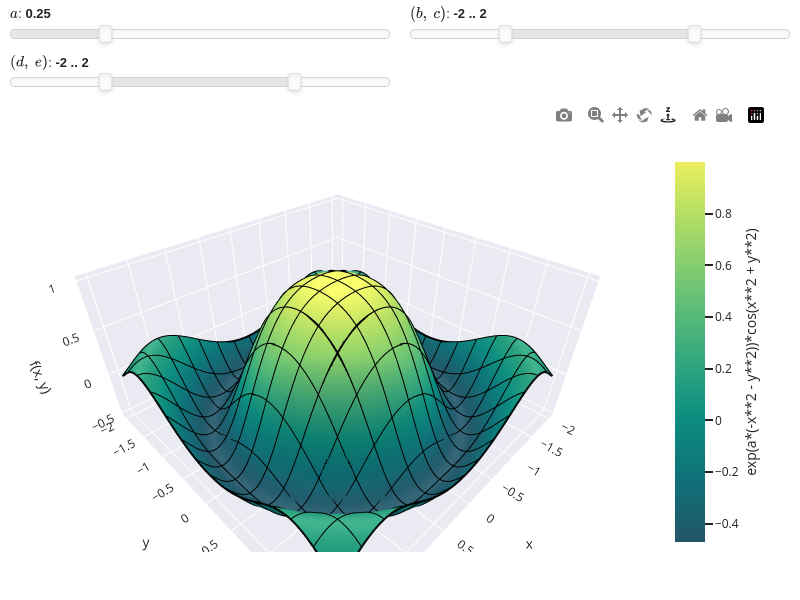
Interactive-widget plot. Refer to the interactive sub-module documentation to learn more about the params dictionary. This plot illustrates:

• the use of prange (parametric plotting range).

• the use of the params dictionary to specify sliders in their basic form: (default, min, max).

• the use of panel.widgets.slider.RangeSlider, which is a 2-values widget.

from sympy import *
from spb import *
import panel as pn
x, y, a, b, c, d, e = symbols("x y a b c d e")
graphics(
    surface(
        cos(x**2 + y**2) * exp(-(x**2 + y**2) * a),
        prange(x, b, c), prange(y, d, e),
        params={
            a: (0.25, 0, 1),
            (b, c): pn.widgets.RangeSlider(
                value=(-2, 2), start=-4, end=4, step=0.1),
            (d, e): pn.widgets.RangeSlider(
                value=(-2, 2), start=-4, end=4, step=0.1),
        },
        use_cm=True, n=100,
        wireframe=True, wf_n1=15, wf_n2=15),
    backend=PB, aspect=dict(x=1.5, y=1.5, z=0.75))

(Source code, small.png)

spb.graphics.functions_3d.surface_parametric(expr1, expr2, expr3, range1=None, range2=None, label=None, rendering_kw=None, **kwargs)

Creates a 3D parametric surface.

Parameters:

expr1, expr2, expr3: Expr or callable

Expression representing the function along x. It can be a:

• Symbolic expression.

• Numerical function of two variable, f(u, v), supporting vectorization. In this case the following keyword arguments are not supported: params.

range1, range2: (symbol, min, max)

A 3-tuple denoting the range of the parameters.

labelstr, optional

The label to be shown in the colorbar. If not provided, the string representation of the expression will be used.

rendering_kwdict, optional

A dictionary of keywords/values which is passed to the backend’s function to customize the appearance of surfaces. Refer to the plotting library (backend) manual for more informations.

colorbarboolean, optional

Show/hide the colorbar. Default to True (colorbar is visible). Only works when use_cm=True.

color_funccallable, optional

Define the surface color mapping when use_cm=True. It can either be:

• A numerical function supporting vectorization. The arity can be:

  • 1 argument: f(u), where u is the first parameter.

  • 2 arguments: f(u, v) where u, v are the parameters.

  • 3 arguments: f(x, y, z) where x, y, z are the coordinates of the points.

  • 5 arguments: f(x, y, z, u, v).

• A symbolic expression having at most as many free symbols as expr_x or expr_y or expr_z.

• None: the default value (color mapping applied to the z-value of the surface).

force_real_evalboolean, optional

Default to False, with which the numerical evaluation is attempted over a complex domain, which is slower but produces correct results. Set this to True if performance is of paramount importance, but be aware that it might produce wrong results. It only works with adaptive=False.

n, n1, n2int, optional

Number of discretization points along the two ranges. Default to 100. n is a shortcut to set the same number of discretization points on both directions.

paramsdict

A dictionary mapping symbols to parameters. This keyword argument enables the interactive-widgets plot. Learn more by reading the documentation of the interactive sub-module.

tx, ty, tzcallable, optional

Apply a numerical function to the discretized domain in the x, y and z direction, respectively.

use_cmboolean, optional

If True, apply a color map to the surface. If False, solid colors will be used instead. Default to False.

wireframeboolean, optional

Enable or disable a wireframe over the surface. Depending on the number of wireframe lines (see wf_n1 and wf_n2), activating this option might add a considerable overhead during the plot’s creation. Default to False (disabled).

wf_n1, wf_n2int, optional

Number of wireframe lines along the two ranges, respectively. Default to 10. Note that increasing this number might considerably slow down the plot’s creation.

wf_npointsint or None, optional

Number of discretization points for the wireframe lines. Default to None, meaning that each wireframe line will have n1 or n2 number of points, depending on the line direction.

wf_rendering_kwdict, optional

A dictionary of keywords/values which is passed to the backend’s function to customize the appearance of wireframe lines.

Returns:

serieslist

A list containing one instance of ParametricSurfaceSeries and possibly multiple instances of Parametric3DLineSeries, if wireframe=True.

See also

surface, surface_spherical, surface_revolution, wireframe

Examples

>>> from sympy import symbols, cos, sin, pi, I, sqrt, atan2, re, im
>>> from spb import *
>>> u, v = symbols('u v')

(Source code)

Plot a parametric surface:

>>> graphics(
...     surface_parametric(
...         u * cos(v), u * sin(v), u * cos(4 * v) / 2,
...         (u, 0, pi), (v, 0, 2*pi), use_cm=False),
...     title="Sinusoidal Cone")
Plot object containing:
[0]: parametric cartesian surface: (u*cos(v), u*sin(v), u*cos(4*v)/2) for u over (0.0, 3.141592653589793) and v over (0.0, 6.283185307179586)

(Source code, png)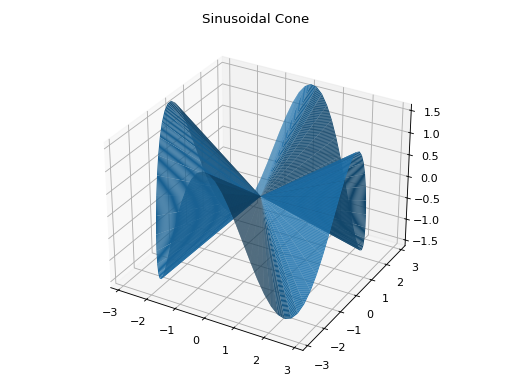

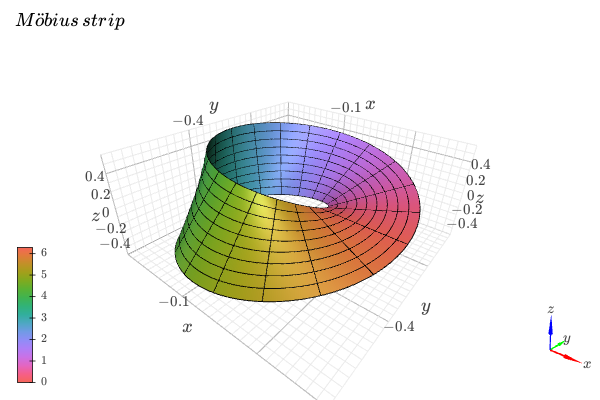
Customize the appearance of the surface by changing the colormap. Apply a color function mapping the v values. Activate the wireframe to better visualize the parameterization.

from sympy import *
from spb import *
import k3d
var("u, v")

x = (1 + v / 2 * cos(u / 2)) * cos(u)
y = (1 + v / 2 * cos(u / 2)) * sin(u)
z = v / 2 * sin(u / 2)
graphics(
    surface_parametric(x, y, z, (u, 0, 2*pi), (v, -1, 1),
        "v", {"color_map": k3d.colormaps.paraview_color_maps.Hue_L60},
        use_cm=True, color_func=lambda u, v: u,
        wireframe=True, wf_n1=20, wf_rendering_kw={"width": 0.004}),
    backend=KB, title=r"Möbius \, strip")

(Source code, small.png)

Riemann surfaces of the real part of the multivalued function z**n, using Plotly:

from sympy import symbols, sqrt, re, im, pi, atan2, sin, cos, I
from spb import *
r, theta, x, y = symbols("r, theta, x, y", real=True)
mag = lambda z: sqrt(re(z)**2 + im(z)**2)
phase = lambda z, k=0: atan2(im(z), re(z)) + 2 * k * pi
n = 2 # exponent (integer)
z = x + I * y # cartesian
d = {x: r * cos(theta), y: r * sin(theta)} # cartesian to polar
branches = [(mag(z)**(1 / n) * cos(phase(z, i) / n)).subs(d)
    for i in range(n)]
exprs = [(r * cos(theta), r * sin(theta), rb) for rb in branches]
series = [
    surface_parametric(*e, (r, 0, 3), (theta, -pi, pi),
        label="branch %s" % (i + 1), wireframe=True, wf_n2=20)
    for i, e in enumerate(exprs)]
graphics(*series, backend=PB, zlabel="f(z)")

(Source code, png)

Plotting a numerical function instead of a symbolic expression.

from spb import *
import numpy as np
fx = lambda u, v: (4 + np.cos(u)) * np.cos(v)
fy = lambda u, v: (4 + np.cos(u)) * np.sin(v)
fz = lambda u, v: np.sin(u)
graphics(
    surface_parametric(fx, fy, fz, ("u", 0, 2 * np.pi),
        ("v", 0, 2 * np.pi)),
    zlim=(-2.5, 2.5), title="Torus", backend=KB, grid=False)

(Source code, small.png)

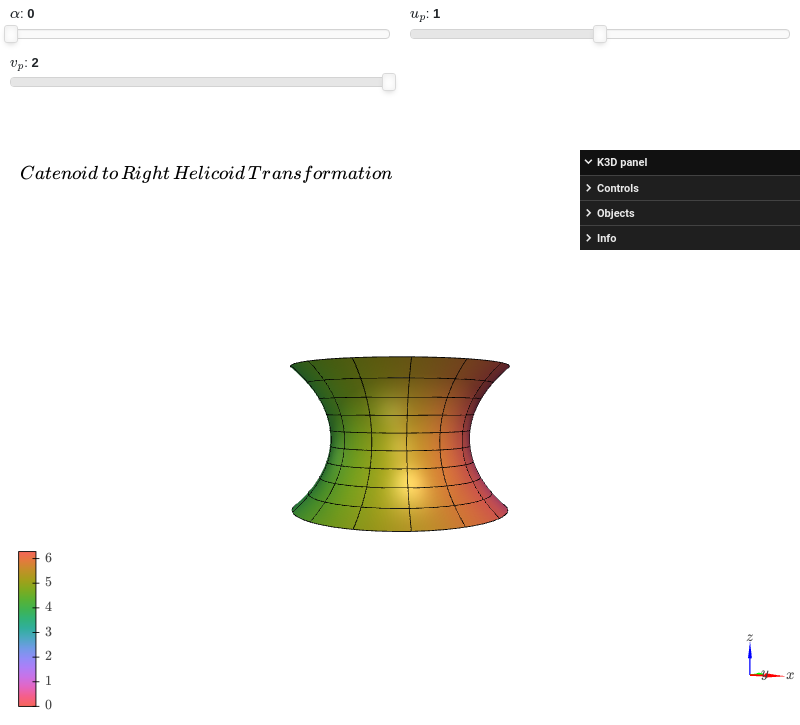
Interactive-widget plot. Refer to the interactive sub-module documentation to learn more about the params dictionary. This plot illustrates:

• the use of prange (parametric plotting range).

• the use of the params dictionary to specify sliders in their basic form: (default, min, max).

from sympy import *
from spb import *
import k3d
alpha, u, v, up, vp = symbols("alpha u v u_p v_p")
graphics(
    surface_parametric(
        exp(u) * cos(v - alpha) / 2 + exp(-u) * cos(v + alpha) / 2,
        exp(u) * sin(v - alpha) / 2 + exp(-u) * sin(v + alpha) / 2,
        cos(alpha) * u + sin(alpha) * v,
        prange(u, -up, up), prange(v, 0, vp * pi),
        n=50, use_cm=True, color_func=lambda u, v: v,
        rendering_kw={"color_map": k3d.colormaps.paraview_color_maps.Hue_L60},
        wireframe=True, wf_n2=15, wf_rendering_kw={"width": 0.005},
        params={
            alpha: (0, 0, pi),
            up: (1, 0, 2),
            vp: (2, 0, 2),
        }),
    backend=KB, grid=False,
    title=r"Catenoid \, to \, Right \, Helicoid \, Transformation"
)

(Source code, small.png)

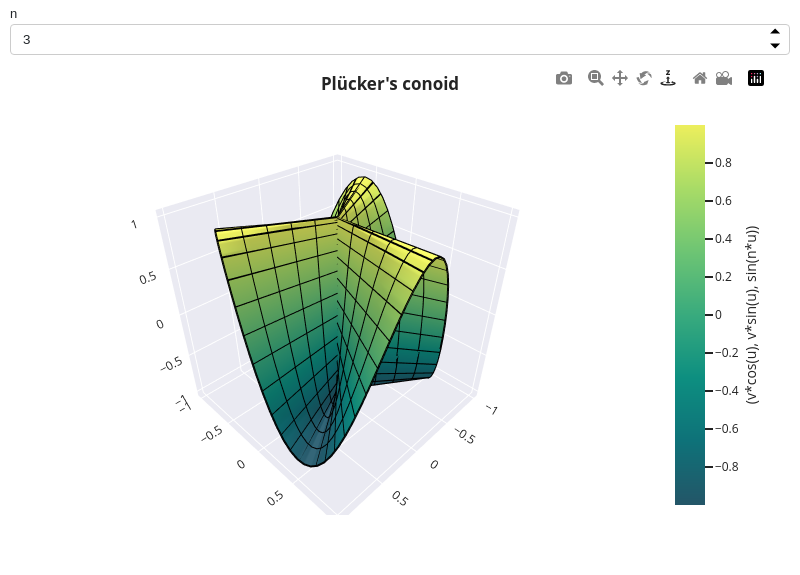
Interactive-widget plot. Refer to the interactive sub-module documentation to learn more about the params dictionary. Note that the plot’s creation might be slow due to the wireframe lines.

from sympy import *
from spb import *
import panel as pn
n, u, v = symbols("n, u, v")
x = v * cos(u)
y = v * sin(u)
z = sin(n * u)
graphics(
    surface_parametric(x, y, z, (u, 0, 2*pi), (v, -1, 0),
        params = {
            n: pn.widgets.IntInput(value=3, name="n")
        },
        use_cm=True, wireframe=True, wf_n1=75, wf_n2=6),
    backend=PB,
    title="Plücker's conoid",
    imodule="panel"
)

(Source code, small.png)

spb.graphics.functions_3d.surface_revolution(curve, range_t, range_phi=None, axis=(0, 0), parallel_axis='z', show_curve=False, curve_kw={}, **kwargs)

Creates a surface of revolution by rotating a curve around an axis of rotation.

Parameters:

curveExpr, list/tuple of 2 or 3 elements

The curve to be revolved, which can be either:

• a symbolic expression

• a 2-tuple representing a parametric curve in 2D space

• a 3-tuple representing a parametric curve in 3D space

range_t(symbol, min, max)

A 3-tuple denoting the range of the parameter of the curve.

range_phi(symbol, min, max)

A 3-tuple denoting the range of the azimuthal angle where the curve will be revolved. Default to (phi, 0, 2*pi).

axis(coord1, coord2)

A 2-tuple that specifies the position of the rotation axis. Depending on the value of parallel_axis:

• "x": the rotation axis intersects the YZ plane at (coord1, coord2).

• "y": the rotation axis intersects the XZ plane at (coord1, coord2).

• "z": the rotation axis intersects the XY plane at (coord1, coord2).

Default to (0, 0).

parallel_axisstr

Specify the axis parallel to the axis of rotation. Must be one of the following options: “x”, “y” or “z”. Default to “z”.

show_curvebool

Add the initial curve to the plot. Default to False.

curve_kwdict

A dictionary of options that will be passed to plot3d_parametric_line if show_curve=True in order to customize the appearance of the initial curve. Refer to its documentation for more information.

**kwargs

Keyword arguments are the same as surface_parametric(). Refer to its documentation for a for a full list of keyword arguments.

Returns:

serieslist

A list containing one instance of ParametricSurfaceSeries, possibly multiple instances of Parametric3DLineSeries representing wireframe lines (if wireframe=True) and possible another instance of Parametric3DLineSeries representing the curve (if show_curve=True).

See also

surface, surface_spherical, surface_parametric, wireframe

Examples

>>> from sympy import symbols, cos, sin, pi
>>> from spb import *
>>> t, phi = symbols('t phi')

(Source code)

Revolve a function around the z axis:

graphics(
    surface_revolution(
        cos(t), (t, 0, pi),
        use_cm=True, color_func=lambda t, phi: phi,
        rendering_kw={"alpha": 0.6, "cmap": "twilight"},
        # indicates the azimuthal angle on the colorbar label
        label=r"$\phi$ [rad]",
        show_curve=True,
        # this dictionary will be passes to plot3d_parametric_line in
        # order to draw the initial curve
        curve_kw=dict(rendering_kw={"color": "r", "label": "cos(t)"}),
        # activate the wireframe to visualize the parameterization
        wireframe=True, wf_n1=15, wf_n2=15,
        wf_rendering_kw={"lw": 0.5, "alpha": 0.75}
    )
)

(Source code, png)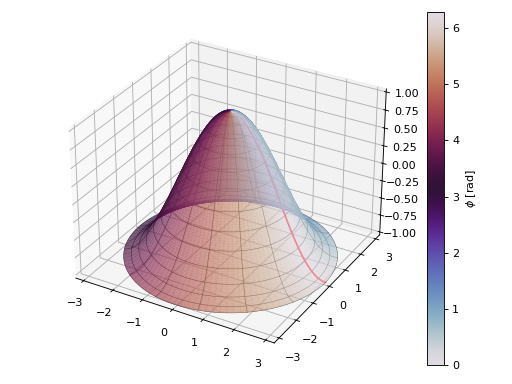

Revolve the same function around an axis parallel to the x axis, using Plotly:

from sympy import symbols, cos, sin, pi
from spb import *
t, phi = symbols('t phi')
graphics(
    surface_revolution(
        cos(t), (t, 0, pi), parallel_axis="x", axis=(1, 0),
        label="phi [rad]", rendering_kw={"colorscale": "twilight"},
        use_cm=True, color_func=lambda t, phi: phi,
        show_curve=True,
        curve_kw=dict(rendering_kw={"line": {"color": "red", "width": 8},
            "name": "cos(t)"}),
        wireframe=True, wf_n1=15, wf_n2=15,
        wf_rendering_kw={"line_width": 1}
    ),
    backend=PB
)

(Source code, png)

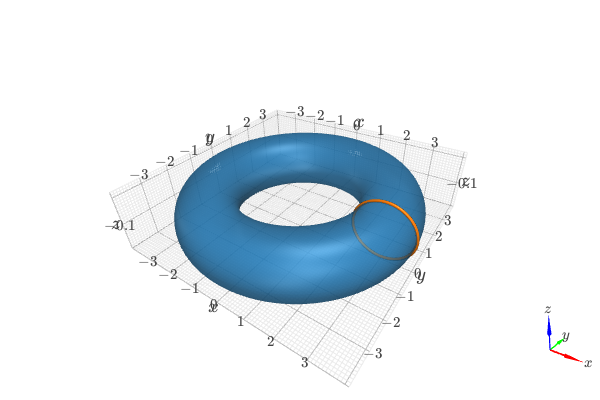
Revolve a 2D parametric circle around the z axis:

from sympy import *
from spb import *
t = symbols("t")
circle = (3 + cos(t), sin(t))
graphics(
    surface_revolution(circle, (t, 0, 2 * pi),
        show_curve=True, rendering_kw={"opacity": 0.65},
        curve_kw={"rendering_kw": {"width": 0.05}}),
    backend=KB)

(Source code, small.png)

Revolve a 3D parametric curve around the z axis for a given azimuthal angle, using Plotly:

from sympy import *
from spb import *
t = symbols("t")
graphics(
    surface_revolution(
        (cos(t), sin(t), t), (t, 0, 2*pi), (phi, 0, pi),
        use_cm=True, color_func=lambda t, phi: t, label="t [rad]",
        show_curve=True,
        wireframe=True, wf_n1=2, wf_n2=5),
    backend=PB, aspect="cube")

(Source code, png)

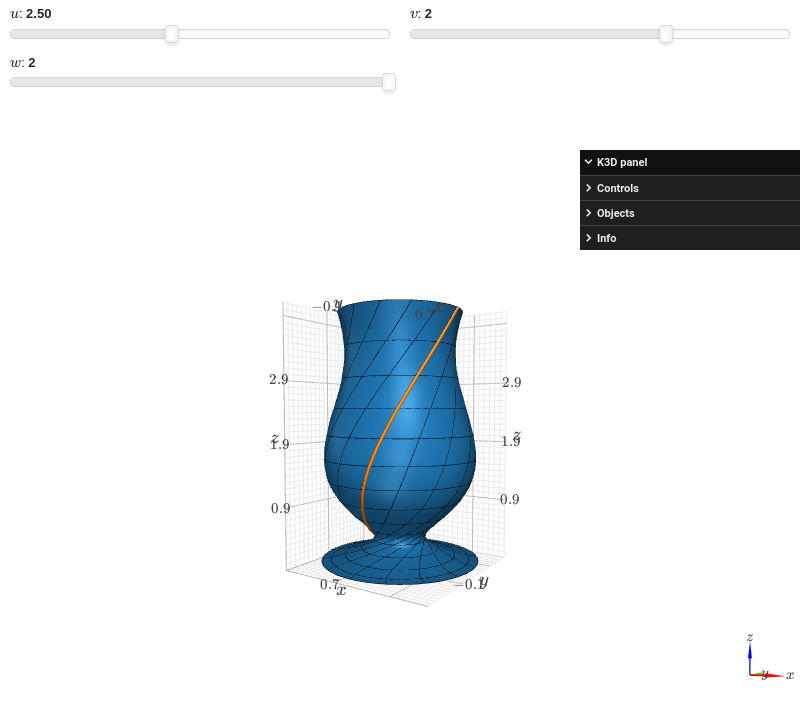
Interactive-widget plot of a goblet. Refer to the interactive sub-module documentation to learn more about the params dictionary. This plot illustrates:

• the use of prange (parametric plotting range).

• the use of the params dictionary to specify sliders in their basic form: (default, min, max).

from sympy import *
from spb import *
t, phi, u, v, w = symbols("t phi u v w")
graphics(
    surface_revolution(
        (t, cos(u * t), t**2), prange(t, 0, v), prange(phi, 0, w*pi),
        axis=(1, 0.2), n=50,
        wireframe=True, wf_n1=15, wf_n2=15,
        wf_rendering_kw={"width": 0.004},
        show_curve=True, curve_kw={"rendering_kw": {"width": 0.025}},
        params={
            u: (2.5, 0, 6),
            v: (2, 0, 3),
            w: (2, 0, 2)
        }),
    backend=KB, force_real_eval=True)

(Source code, small.png)

spb.graphics.functions_3d.surface_spherical(r, range_theta=None, range_phi=None, label=None, rendering_kw=None, **kwargs)

Plots a radius as a function of the spherical coordinates theta and phi.

Parameters:

r: Expr or callable

Expression representing the radius. It can be a:

• Symbolic expression.

• Numerical function of two variable, f(theta, phi), supporting vectorization. In this case the following keyword arguments are not supported: params.

range_theta: (symbol, min, max)

A 3-tuple denoting the range of the polar angle, which is limited in [0, pi]. Consider a sphere:

• theta=0 indicates the north pole.

• theta=pi/2 indicates the equator.

• theta=pi indicates the south pole.

range_phi: (symbol, min, max)

A 3-tuple denoting the range of the azimuthal angle, which is limited in [0, 2*pi].

labelstr, optional

The label to be shown in the colorbar. If not provided, the string representation of the expression will be used.

rendering_kwdict, optional

A dictionary of keywords/values which is passed to the backend’s function to customize the appearance of surfaces. Refer to the plotting library (backend) manual for more informations.

**kwargs

Keyword arguments are the same as surface_parametric(). Refer to its documentation for a for a full list of keyword arguments.

Returns:

serieslist

A list containing one instance of ParametricSurfaceSeries and possibly multiple instances of Parametric3DLineSeries, if wireframe=True.

See also

surface, surface_parametric, surface_revolution, wireframe

Examples

>>> from sympy import symbols, cos, sin, pi, Ynm, re, lambdify
>>> from spb import *
>>> theta, phi = symbols('theta phi')

(Source code)

Sphere cap:

>>> graphics(
...     surface_spherical(1, (theta, 0, 0.7 * pi), (phi, 0, 1.8 * pi)))
Plot object containing:
[0]: parametric cartesian surface: (sin(theta)*cos(phi), sin(phi)*sin(theta), cos(theta)) for theta over (0.0, 2.199114857512855) and phi over (0.0, 5.654866776461628)

(Source code, png)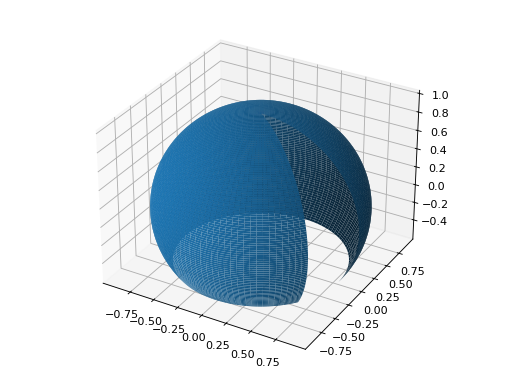

Plot real spherical harmonics, highlighting the regions in which the real part is positive and negative, using Plotly:

from sympy import symbols, sin, pi, Ynm, re, lambdify
from spb import *
theta, phi = symbols('theta phi')
r = re(Ynm(3, 3, theta, phi).expand(func=True).rewrite(sin).expand())
graphics(
    surface_spherical(
        abs(r), (theta, 0, pi), (phi, 0, 2 * pi), "real",
        use_cm=True, n2=200,
        color_func=lambdify([theta, phi], r)),
    backend=PB)

(Source code, png)

Multiple surfaces with wireframe lines, using Plotly. Note that activating the wireframe option might add a considerable overhead during the plot’s creation.

from sympy import symbols, sin, pi
from spb import *
theta, phi = symbols('theta phi')
r1 = 1
r2 = 1.5 + sin(5 * phi) * sin(10 * theta) / 10
graphics(
    surface_spherical(r1, (theta, 0, pi / 2), (phi, 0.35 * pi, 2 * pi),
        label="r1", wireframe=True, wf_n2=25),
    surface_spherical(r2, (theta, 0, pi / 2), (phi, 0.35 * pi, 2 * pi),
        label="r2", wireframe=True, wf_n2=25),
    backend=PB)

(Source code, png)

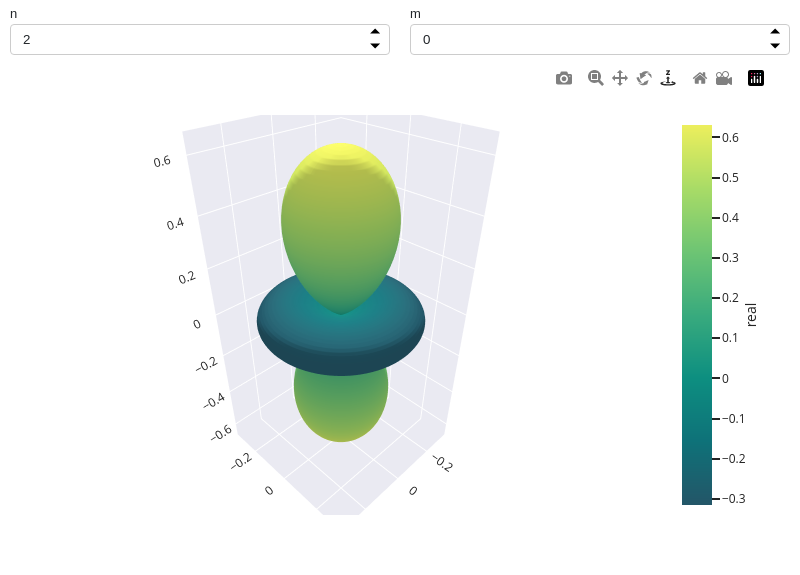
Interactive-widget plot of real spherical harmonics, highlighting the regions in which the real part is positive and negative. Note that the plot’s creation and update might be slow and that it must be m < n at all times. Refer to the interactive sub-module documentation to learn more about the params dictionary.

from sympy import *
from spb import *
import panel as pn
n, m = symbols("n, m")
phi, theta = symbols("phi, theta", real=True)
r = re(Ynm(n, m, theta, phi).expand(func=True).rewrite(sin).expand())
graphics(
    surface_spherical(abs(r), (theta, 0, pi), (phi, 0, 2*pi),
        label="real",
        params = {
            n: pn.widgets.IntInput(value=2, name="n"),
            m: pn.widgets.IntInput(value=0, name="m"),
        },
        use_cm=True, color_func=r, force_real_eval=True),
    backend=PB, imodule="panel")

(Source code, small.png)

spb.graphics.functions_3d.plane(p, range1=None, range2=None, range3=None, label=None, rendering_kw=None, **kwargs)

Plot a plane in a 3D space.

Parameters:

pPlane

range1, range2, range3(symbol, min, max)

A 3-tuple denoting the range of a particular variable.

labelstr, optional

An optional string denoting the label of the expression to be visualized on the legend. If not provided, the string representation of the expression will be used.

rendering_kwdict, optional

A dictionary of keywords/values which is passed to the backend’s function to customize the appearance of lines. Refer to the plotting library (backend) manual for more informations.

**kwargs

Keyword arguments are the same as surface(). Refer to its documentation for a for a full list of keyword arguments.

Returns:

serieslist

A list containing an instance of PlaneSeries.

See also

surface

Examples

from sympy import *
from spb import *
from sympy.abc import x, y, z
ranges = [(x, -5, 5), (y, -5, 5), (z, -5, 5)]
graphics(
    plane(Plane((0, 0, 0), (1, 0, 0)), *ranges, label="yz"),
    plane(Plane((0, 0, 0), (0, 1, 0)), *ranges, label="xz"),
    plane(Plane((0, 0, 0), (0, 0, 1)), *ranges, label="yz"),
    plane(Plane((0, 0, 0), (1, 1, 1)), *ranges, label="inclined", n=150),
    backend=PB, xlabel="x", ylabel="y", zlabel="z"
)

(Source code, png)

spb.graphics.functions_3d.implicit_3d(expr, range1=None, range2=None, range3=None, label=None, rendering_kw=None, **kwargs)

Plots an isosurface of a function.

Parameters:

expr: Expr or callable

Implicit expression. It can be a:

• Symbolic expression.

• Numerical function of three variable, f(x, y, z), supporting

  vectorization.

range1, range2, range3: (symbol, min, max)

A 3-tuple denoting the range of a particular variable.

labelstr, optional

The label to be shown in the colorbar. If not provided, the string representation of the expression will be used.

rendering_kwdict, optional

A dictionary of keywords/values which is passed to the backend’s function to customize the appearance of surfaces. Refer to the plotting library (backend) manual for more informations.

n, n1, n2, n3int, optional

Number of discretization points along the three ranges. Default to 100. n is a shortcut to set the same number of discretization points on all directions.

Returns:

serieslist

A list containing one instance of Implicit3DSeries.

See also

surface, spb.graphics.functions_2d.implicit_2d

Notes

1. the number of discretization points is crucial as the algorithm will discretize a volume. A high number of discretization points creates a smoother mesh, at the cost of a much higher memory consumption and slower computation.

2. Only PlotlyBackend and K3DBackend support 3D implicit plotting.

3. To plot f(x, y, z) = c either write expr = f(x, y, z) - c or pass the appropriate keyword to rendering_kw. Read the backends documentation to find out the available options.

Examples

from sympy import symbols
from spb import *
x, y, z = symbols('x, y, z')
graphics(
    implicit_3d(x**2 + y**3 - z**2, (x, -2, 2), (y, -2, 2), (z, -2, 2)),
    backend=PB)

(Source code, png)

graphics(
    implicit_3d(x**4 + y**4 + z**4 - (x**2 + y**2 + z**2 - 0.3),
        (x, -2, 2), (y, -2, 2), (z, -2, 2)),
    backend=PB)

(Source code, png)

Visualize the isocontours from isomin=0 to isomax=2 by providing a rendering_kw dictionary:

graphics(
    implicit_3d(1/x**2 - 1/y**2 + 1/z**2,
        (x, -2, 2), (y, -2, 2), (z, -2, 2),
        rendering_kw={
            "isomin": 0, "isomax": 2,
            "colorscale":"aggrnyl", "showscale":True
        }),
    backend=PB
)

(Source code, png)

spb.graphics.functions_3d.wireframe(surface_series, n1=10, n2=10, n=None, rendering_kw=None, **kwargs)

Creates a wireframe of a 3D surface.

Parameters:

surface_seriesBaseSeries

A data series representing a surface.

n1, n2: int, optional

Number of wireframe lines along each direction (or range).

nint, optional

Number of evaluation points for each wireframe line. If not provided, the algorithm will chose the number of discretization points from the surface_series. The higher this number, the slower the creation of the plot.

rendering_kwdict, optional

A dictionary of keywords/values which is passed to the backend’s function to customize the appearance of surfaces. Refer to the plotting library (backend) manual for more informations.

**kwargs

Keyword arguments are the same as line_parametric_3d(). Refer to its documentation for a for a full list of keyword arguments.

Returns:

serieslist

A list containing instances of Parametric3DLineSeries.

See also

surface, surface_parametric, surface_spherical, surface_revolution

Examples

Provide better code separation between the surface and wireframe:

from sympy import *
from spb import *
import numpy as np
x, y = symbols("x y")
surf_series = surface(
    cos(x*y) * exp(-sqrt(x**2 + y**2) / 4), (x, -pi, pi), (y, -pi, pi),
    use_cm=True, color_func=lambda x, y, z: np.sqrt(x**2 + y**2)
)
graphics(
    surf_series,
    wireframe(surf_series[0], n1=11, n2=11),
    backend=PB, aspect=dict(x=1.5, y=1.5, z=1)
)

(Source code, png)

Show wireframe without showing the actual surface. Here, dotted wireframe represent the half-unit sphere.

from sympy import *
from spb import *
var("t u v theta phi")
r_sphere = 1
sphere = surface_spherical(1, (theta, 0, pi), (phi, pi, 2*pi))[0]
t = pi / 3 # half-cone angle
r_cone = r_sphere * sin(t)
graphics(
    wireframe(sphere, n1=13, rendering_kw={"line_dash": "dot"}),
    surface_spherical(1, (theta, pi - t, pi), (phi, pi, 2*pi),
        label="sphere cap", wireframe=True, wf_n1=5),
    surface_parametric(
        u * cos(v), u * sin(v), -u / tan(t), (u, 0, r_cone), (v, pi , 2*pi),
        label="cone", wireframe=True, wf_n1=7),
    backend=PB, grid=False
)

(Source code, png)