Complex Analysis

NOTE: For technical reasons, all interactive-widgets plots in this documentation are created using Holoviz’s Panel. Often, they will ran just fine with ipywidgets too. However, if a specific example uses the param library, or widgets from the panel module, then users will have to modify the params dictionary in order to make it work with ipywidgets. Refer to Interactive module for more information.

spb.graphics.complex_analysis.complex_points(*numbers, label=None, rendering_kw=None, scatter=True, **kwargs)

Plot complex points.

Parameters:

*numbers

Complex numbers, or a list of complex numbers.

labelstr, optional

The label to be shown in the legend. If not provided, the string representation of expr1 and expr1 will be used.

rendering_kwdict, optional

A dictionary of keywords/values which is passed to the backend’s function to customize the appearance of lines. Refer to the plotting library (backend) manual for more informations.

scatterboolean, optional

Default to True, which renders a scatter plot. If False, a line will connect all the points.

paramsdict

A dictionary mapping symbols to parameters. This keyword argument enables the interactive-widgets plot. Learn more by reading the documentation of the interactive sub-module.

Returns:

serieslist

A list containing an instance of ComplexPointSeries.

Examples

>>> from sympy import I, symbols, exp, sqrt, cos, sin, pi, gamma
>>> from spb import *
>>> x, y, z = symbols('x, y, z')

(Source code)

Plot individual complex points:

>>> graphics(complex_points(3 + 2 * I, 4 * I, 2))
Plot object containing:
[0]: complex points: (3 + 2*I, 4*I, 2)

(Source code, png)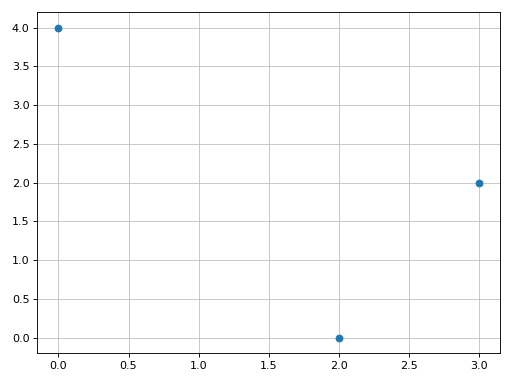

Plot two lists of complex points and assign to them custom labels:

>>> expr1 = z * exp(2 * pi * I * z)
>>> expr2 = 2 * expr1
>>> n = 15
>>> l1 = [expr1.subs(z, t / n) for t in range(n)]
>>> l2 = [expr2.subs(z, t / n) for t in range(n)]
>>> graphics(
...     complex_points(l1, label="f1"),
...     complex_points(l2, label="f2"), legend=True)
Plot object containing:
[0]: complex points: (0.0, 0.0666666666666667*exp(0.133333333333333*I*pi), 0.133333333333333*exp(0.266666666666667*I*pi), 0.2*exp(0.4*I*pi), 0.266666666666667*exp(0.533333333333333*I*pi), 0.333333333333333*exp(0.666666666666667*I*pi), 0.4*exp(0.8*I*pi), 0.466666666666667*exp(0.933333333333333*I*pi), 0.533333333333333*exp(1.06666666666667*I*pi), 0.6*exp(1.2*I*pi), 0.666666666666667*exp(1.33333333333333*I*pi), 0.733333333333333*exp(1.46666666666667*I*pi), 0.8*exp(1.6*I*pi), 0.866666666666667*exp(1.73333333333333*I*pi), 0.933333333333333*exp(1.86666666666667*I*pi))
[1]: complex points: (0, 0.133333333333333*exp(0.133333333333333*I*pi), 0.266666666666667*exp(0.266666666666667*I*pi), 0.4*exp(0.4*I*pi), 0.533333333333333*exp(0.533333333333333*I*pi), 0.666666666666667*exp(0.666666666666667*I*pi), 0.8*exp(0.8*I*pi), 0.933333333333333*exp(0.933333333333333*I*pi), 1.06666666666667*exp(1.06666666666667*I*pi), 1.2*exp(1.2*I*pi), 1.33333333333333*exp(1.33333333333333*I*pi), 1.46666666666667*exp(1.46666666666667*I*pi), 1.6*exp(1.6*I*pi), 1.73333333333333*exp(1.73333333333333*I*pi), 1.86666666666667*exp(1.86666666666667*I*pi))

(Source code, png)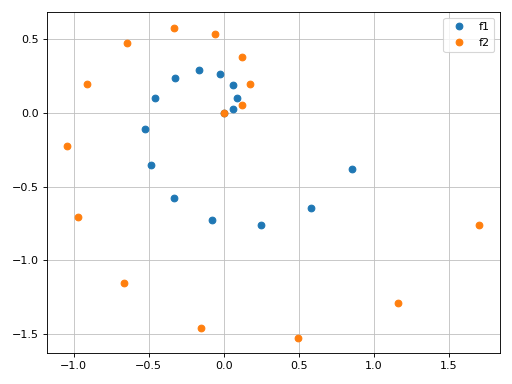

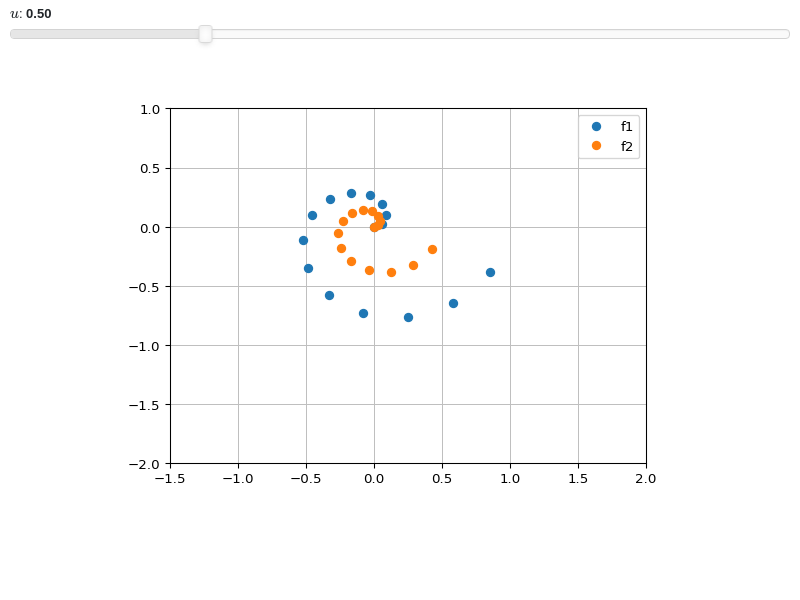
Interactive-widget plot. Refer to the interactive sub-module documentation to learn more about the params dictionary.

from sympy import *
from spb import *
z, u = symbols("z u")
expr1 = z * exp(2 * pi * I * z)
expr2 = u * expr1
n = 15
l1 = [expr1.subs(z, t / n) for t in range(n)]
l2 = [expr2.subs(z, t / n) for t in range(n)]
params = {u: (0.5, 0, 2)}
graphics(
    complex_points(l1, label="f1", params=params),
    complex_points(l2, label="f2", params=params),
    legend=True, xlim=(-1.5, 2), ylim=(-2, 1))

(Source code, small.png)

spb.graphics.complex_analysis.line_abs_arg_colored(expr, range=None, label=None, rendering_kw=None, **kwargs)

Plot the absolute value of a complex function f(x) colored by its argument, with x in Reals.

Parameters:

exprExpr

Symbolic expression representing the function of one variable to be plotted.

range(symbol, min, max)

A 3-tuple denoting the range of the x variable. Default values: min=-10 and max=10.

labelstr, optional

The label to be shown in the legend. If not provided, the string representation of expr will be used.

rendering_kwdict, optional

A dictionary of keywords/values which is passed to the backend’s function to customize the appearance of lines. Refer to the plotting library (backend) manual for more informations.

**kwargs

Keyword arguments are the same as line(). Refer to its documentation for a for a full list of keyword arguments.

Returns:

serieslist

A list containing an instance of AbsArgLineSeries.

See also

spb.graphics.functions_2d.line, line_abs_arg, line_real_imag

domain_coloring

Examples

>>> from sympy import I, symbols, cos, sin, pi
>>> from spb import *
>>> x = symbols('x')

(Source code)

Plot the modulus of a complex function colored by its magnitude:

>>> graphics(
...     line_abs_arg_colored(cos(x) + sin(I * x), (x, -2, 2),
...         label="f"))
Plot object containing:
[0]: cartesian abs-arg line: cos(x) + I*sinh(x) for x over ((-2+0j), (2+0j))

(Source code, png)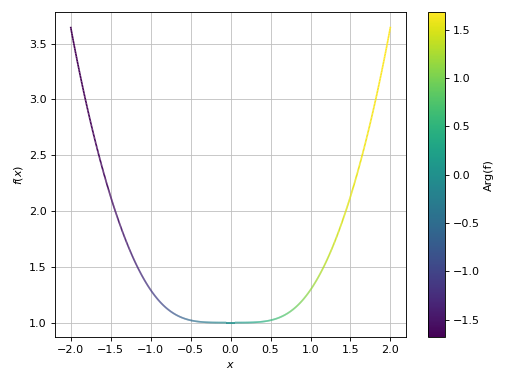

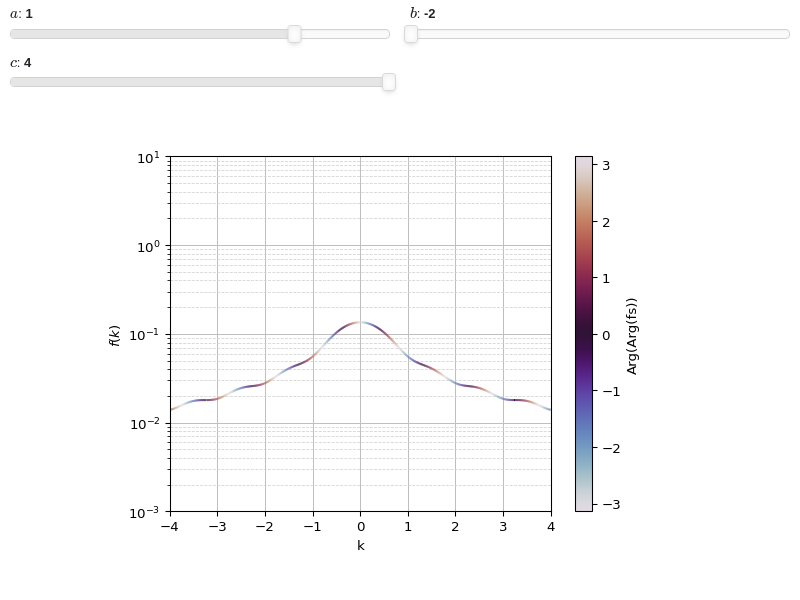
Interactive-widget plot of a Fourier Transform. Refer to the interactive sub-module documentation to learn more about the params dictionary. This plot illustrates:

• the use of prange (parametric plotting range).

• for line_abs_arg_colored, symbols going into prange must be real.

• the use of the params dictionary to specify sliders in their basic form: (default, min, max).

from sympy import *
from spb import *
x, k, a, b = symbols("x, k, a, b")
c = symbols("c", real=True)
f = exp(-x**2) * (Heaviside(x + a) - Heaviside(x - b))
fs = fourier_transform(f, x, k)
graphics(
    line_abs_arg_colored(fs, prange(k, -c, c),
        params={a: (1, -2, 2), b: (-2, -2, 2), c: (4, 0.5, 4)},
        label="Arg(fs)"),
    xlabel="k", yscale="log", ylim=(1e-03, 10))

(Source code, small.png)

spb.graphics.complex_analysis.line_abs_arg(expr, range=None, label=None, rendering_kw=None, abs=True, arg=True, **kwargs)

Plot the absolute value and/or the argument of a complex function f(x) with x in Reals.

Parameters:

exprExpr

Symbolic expression representing the function of one variable to be plotted.

range(symbol, min, max)

A 3-tuple denoting the range of the x variable. Default values: min=-10 and max=10.

labelstr, optional

The label to be shown in the legend. If not provided, the string representation of expr will be used.

rendering_kwdict, optional

A dictionary of keywords/values which is passed to the backend’s function to customize the appearance of lines. Refer to the plotting library (backend) manual for more informations.

absboolean, optional

Show/hide the absolute value. Default to True (visible).

argboolean, optional

Show/hide the argument. Default to True (visible).

**kwargs

Keyword arguments are the same as line(). Refer to its documentation for a for a full list of keyword arguments.

Returns:

serieslist

A list containing instances of LineOver1DRangeSeries.

See also

spb.graphics.functions_2d.line, line_real_imag, line_abs_arg_colored

Examples

>>> from sympy import symbols, sqrt, log
>>> from spb import *
>>> x = symbols('x')

(Source code)

Plot only the absolute value and argument:

>>> graphics(
...     line_abs_arg(sqrt(x), (x, -3, 3), label="f"),
...     line_abs_arg(log(x), (x, -3, 3), label="g",
...         rendering_kw={"linestyle": "-."}),
... )
Plot object containing:
[0]: cartesian line: abs(sqrt(x)) for x over (-3.0, 3.0)
[1]: cartesian line: arg(sqrt(x)) for x over (-3.0, 3.0)
[2]: cartesian line: abs(log(x)) for x over (-3.0, 3.0)
[3]: cartesian line: arg(log(x)) for x over (-3.0, 3.0)

(Source code, png)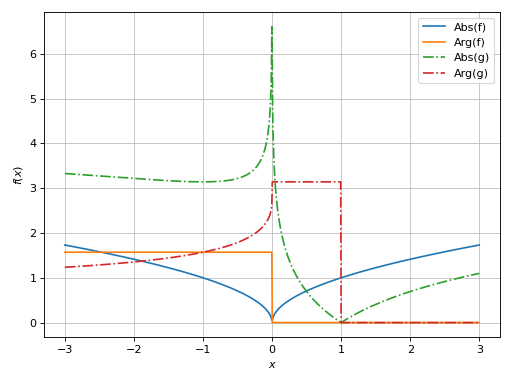

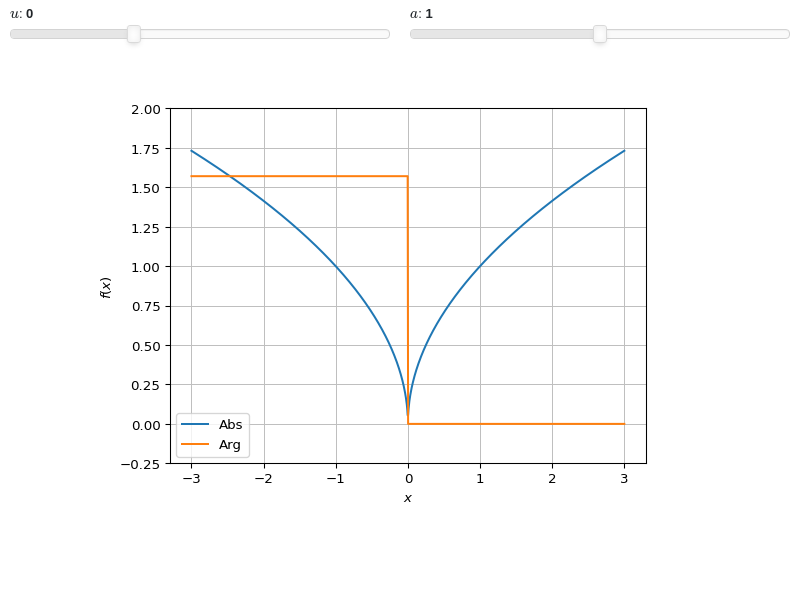
Interactive-widget plot. Refer to the interactive sub-module documentation to learn more about the params dictionary. This plot illustrates:

• the use of prange (parametric plotting range).

• for line_abs_arg, symbols going into prange must be real.

• the use of the params dictionary to specify sliders in their basic form: (default, min, max).

from sympy import *
from spb import *
x, u = symbols("x, u")
a = symbols("a", real=True)
graphics(
    line_abs_arg(
        (sqrt(x) + u) * exp(-u * x**2), prange(x, -3*a, 3*a),
        params={u: (0, -1, 2), a: (1, 0, 2)}),
    ylim=(-0.25, 2))

(Source code, small.png)

spb.graphics.complex_analysis.line_real_imag(expr, range=None, label=None, rendering_kw=None, real=True, imag=True, **kwargs)

Plot the real and imaginary part of a complex function f(x) with x in Reals.

Parameters:

exprExpr

Symbolic expression representing the function of one variable to be plotted.

range(symbol, min, max)

A 3-tuple denoting the range of the x variable. Default values: min=-10 and max=10.

labelstr, optional

The label to be shown in the legend. If not provided, the string representation of expr will be used.

rendering_kwdict, optional

A dictionary of keywords/values which is passed to the backend’s function to customize the appearance of lines. Refer to the plotting library (backend) manual for more informations.

realboolean, optional

Show/hide the real part. Default to True (visible).

imagboolean, optional

Show/hide the imaginary part. Default to True (visible).

**kwargs

Keyword arguments are the same as line(). Refer to its documentation for a for a full list of keyword arguments.

Returns:

serieslist

A list containing instances of LineOver1DRangeSeries.

See also

spb.graphics.functions_2d.line, line_abs_arg, line_abs_arg_colored

Notes

Given a symbolic expression, there are two possible way to create a real/imag plot:

1. Apply Sympy’s re or im to the symbolic expression, then evaluates it.

2. Evaluates the symbolic expression over the provided range in order to get complex values, then extract the real/imaginary parts with Numpy.

For performance reasons, line_real_imag implements the second approach. In fact, SymPy’s re and im functions evaluate their arguments, potentially creating unecessarely long symbolic expressions that requires a lot of time to be evaluated.

Another thing to be aware of is branch cuts of complex-valued functions. The plotting module attempt to evaluate a symbolic expression using complex numbers. Depending on the evaluation module being used, we might get different results. For example, the following two expressions are equal when x > 0:

>>> from sympy import symbols, im, Rational
>>> from spb import *
>>> x = symbols('x', positive=True)
>>> x_generic = symbols("x")
>>> e1 = (1 / x)**(Rational(6, 5))
>>> e2 = x**(-Rational(6, 5))
>>> e2.equals(e1)
True
>>> e3 = (1 / x_generic)**(Rational(6, 5))
>>> e4 = x_generic**(-Rational(6, 5))
>>> e4.equals(e3)
False
>>> graphics(
...     line_real_imag(e3, label="e3", real=False,
...         detect_poles="symbolic"),
...     line_real_imag(e4, label="e4", real=False,
...         detect_poles="symbolic"),
...     ylim=(-5, 5))
Plot object containing:
[0]: cartesian line: im((1/x)**(6/5)) for x over (-10.0, 10.0)
[1]: cartesian line: im(x**(-6/5)) for x over (-10.0, 10.0)

(Source code, png)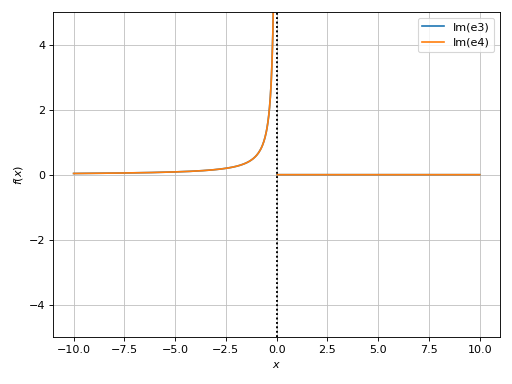

The result computed by the plotting module might feels off: the two expressions are different, but according to the plot they are the same. Someone could say that the imaginary part of e3 or e4 should be negative when x < 0. We can evaluate the expressions with mpmath:

>>> graphics(
...     line_real_imag(e3, label="e3", real=False,
...         detect_poles="symbolic", modules="mpmath"),
...     line_real_imag(e4, label="e4", real=False,
...         detect_poles="symbolic", modules="mpmath"),
...     ylim=(-5, 5))
Plot object containing:
[0]: cartesian line: im((1/x)**(6/5)) for x over (-10.0, 10.0)
[1]: cartesian line: im(x**(-6/5)) for x over (-10.0, 10.0)

(Source code, png)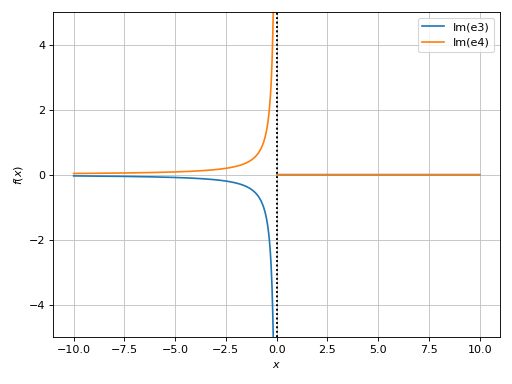

With mpmath we see that e3 and e4 are indeed different.

Examples

>>> from sympy import symbols, sqrt, log
>>> from spb import *
>>> x = symbols('x')

(Source code)

Plot only the absolute value and argument:

>>> graphics(
...     line_real_imag(sqrt(x), (x, -3, 3), label="f"))
Plot object containing:
[0]: cartesian line: re(sqrt(x)) for x over (-3.0, 3.0)
[1]: cartesian line: im(sqrt(x)) for x over (-3.0, 3.0)

(Source code, png)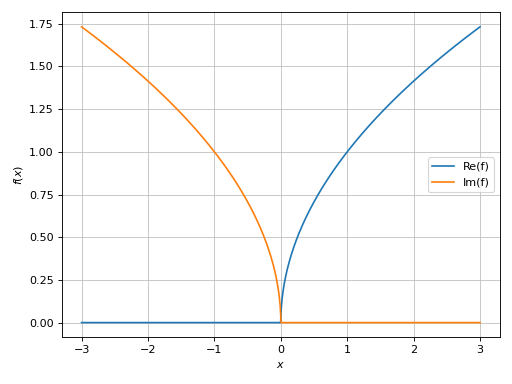

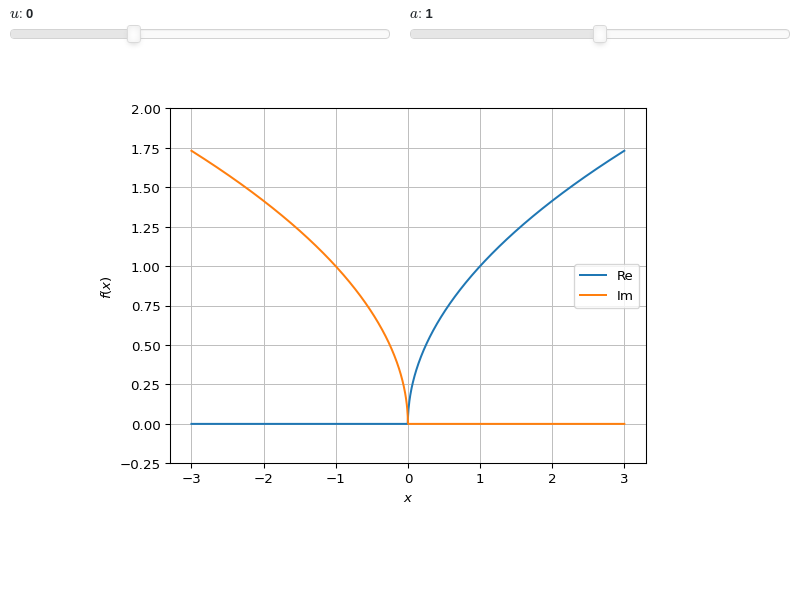
Interactive-widget plot. Refer to the interactive sub-module documentation to learn more about the params dictionary. This plot illustrates:

• the use of prange (parametric plotting range).

• for line_real_imag, symbols going into prange must be real.

• the use of the params dictionary to specify sliders in their basic form: (default, min, max).

from sympy import *
from spb import *
x, u = symbols("x, u")
a = symbols("a", real=True)
graphics(
    line_real_imag((sqrt(x) + u) * exp(-u * x**2), prange(x, -3*a, 3*a),
        params={u: (0, -1, 2), a: (1, 0, 2)}),
    ylim=(-0.25, 2))

(Source code, small.png)

spb.graphics.complex_analysis.surface_abs_arg(expr, range=None, label=None, rendering_kw=None, abs=True, arg=True, **kwargs)

Plot the absolute value and/or the argument of a complex function f(x) with x in Complex.

Parameters:

exprExpr

Symbolic expression representing the function of one variable to be plotted.

range(symbol, min, max)

A 3-tuple denoting the range of the x variable. Default values: min=-10-10j and max=10+10j.

labelstr, optional

The label to be shown in the legend. If not provided, the string representation of expr will be used.

rendering_kwdict, optional

A dictionary of keywords/values which is passed to the backend’s function to customize the appearance of surfaces. Refer to the plotting library (backend) manual for more informations.

absboolean, optional

Show/hide the absolute value. Default to True (visible).

argboolean, optional

Show/hide the argument. Default to True (visible).

**kwargs

Keyword arguments are the same as surface(). Refer to its documentation for a for a full list of keyword arguments.

Returns:

serieslist

A list containing up two to instance of ComplexSurfaceSeries and possibly multiple instances of Parametric3DLineSeries, if wireframe=True.

See also

spb.graphics.functions_3d.surface, contour_abs_arg, surface_real_imag

contour_abs_arg

Examples

>>> from sympy import symbols, sqrt
>>> from spb import *
>>> x = symbols('x')

(Source code)

>>> graphics(
...     surface_abs_arg(sqrt(x), (x, -3-3j, 3+3j), n=101))
Plot object containing:
[0]: complex cartesian surface: abs(sqrt(x)) for re(x) over (-3.0, 3.0) and im(x) over (-3.0, 3.0)
[1]: complex cartesian surface: arg(sqrt(x)) for re(x) over (-3.0, 3.0) and im(x) over (-3.0, 3.0)

(Source code, png)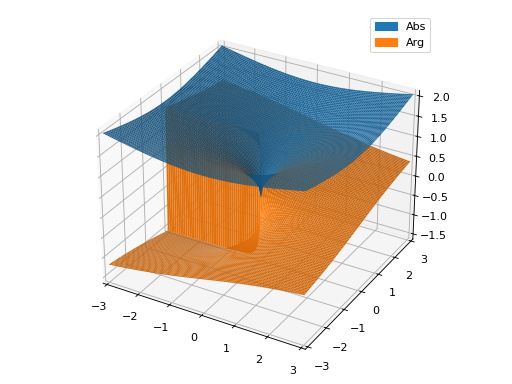

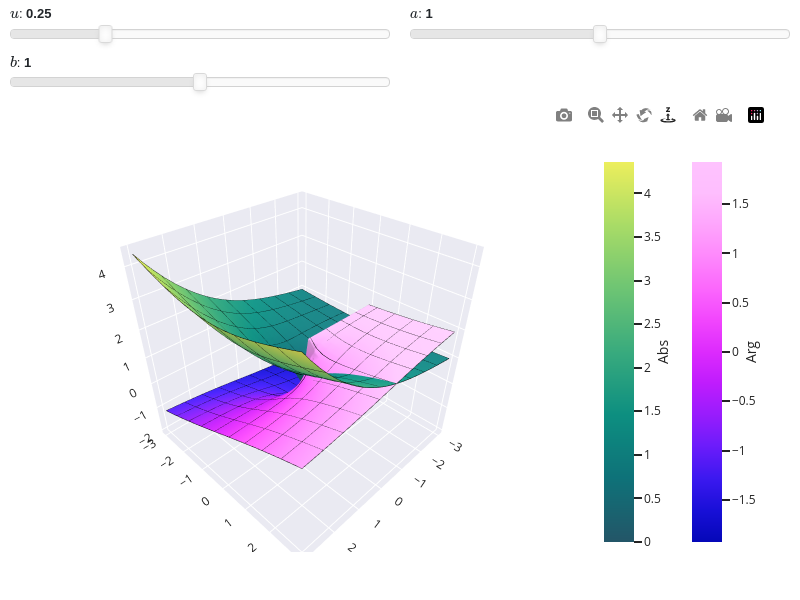
Interactive-widget plot. Refer to the interactive sub-module documentation to learn more about the params dictionary. This plot illustrates:

• the use of prange (parametric plotting range).

• the use of the params dictionary to specify sliders in their basic form: (default, min, max).

from sympy import *
from spb import *
x, u, a, b = symbols("x, u, a, b")
graphics(
    surface_abs_arg(
        sqrt(x) * exp(u * x), prange(x, -3*a-b*3j, 3*a+b*3j),
        n=25, wireframe=True, wf_rendering_kw={"line_width": 1},
        use_cm=True, params={
            u: (0.25, 0, 1),
            a: (1, 0, 2),
            b: (1, 0, 2)
        }),
        backend=PB, aspect="cube")

(Source code, small.png)

spb.graphics.complex_analysis.contour_abs_arg(expr, range=None, label=None, rendering_kw=None, abs=True, arg=True, **kwargs)

Plot contours of the absolute value and/or the argument of a complex function f(x) with x in Complex.

Parameters:

exprExpr

Symbolic expression representing the function of one variable to be plotted.

range(symbol, min, max)

A 3-tuple denoting the range of the x variable. Default values: min=-10-10j and max=10+10j.

labelstr, optional

The label to be shown in the legend. If not provided, the string representation of expr will be used.

rendering_kwdict, optional

A dictionary of keywords/values which is passed to the backend’s function to customize the appearance of contours. Refer to the plotting library (backend) manual for more informations.

absboolean, optional

Show/hide the absolute value. Default to True (visible).

argboolean, optional

Show/hide the argument. Default to True (visible).

**kwargs

Keyword arguments are the same as contour(). Refer to its documentation for a for a full list of keyword arguments.

Returns:

serieslist

A list containing up two to instance of ComplexSurfaceSeries.

See also

spb.graphics.functions_2d.contour, contour_real_imag, surface_real_imag

surface_abs_arg

Examples

>>> from sympy import symbols, sqrt
>>> from spb import *
>>> x = symbols('x')

(Source code)

>>> graphics(
...     contour_abs_arg(sqrt(x), (x, -3-3j, 3+3j), arg=False),
...     grid=False)
Plot object containing:
[0]: complex contour: abs(sqrt(x)) for re(x) over (-3.0, 3.0) and im(x) over (-3.0, 3.0)

(Source code, png)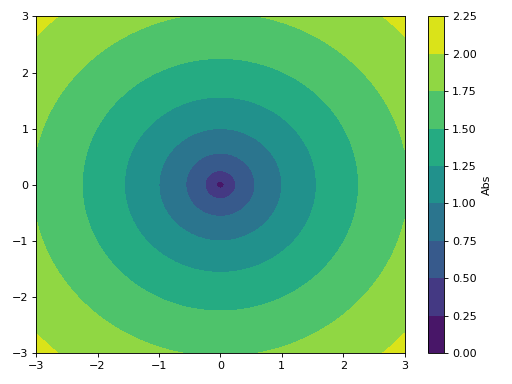

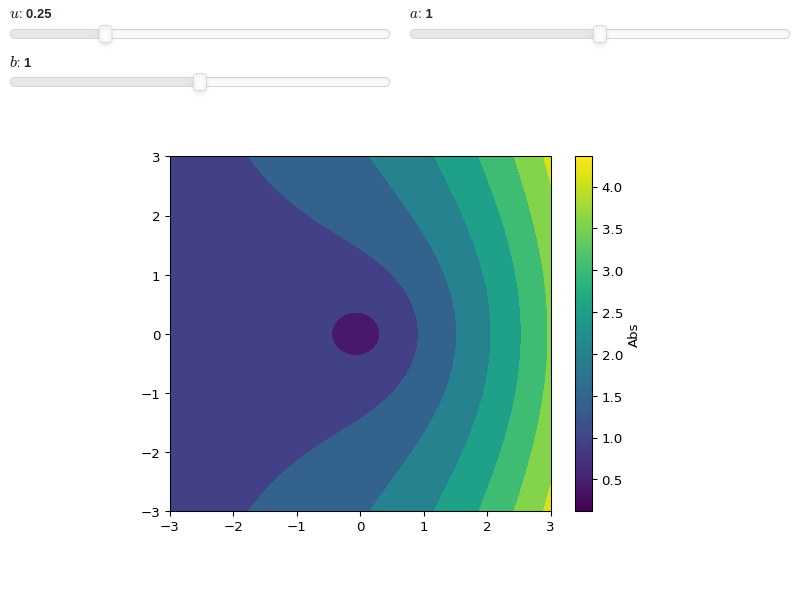
Interactive-widget plot. Refer to the interactive sub-module documentation to learn more about the params dictionary. This plot illustrates:

• the use of prange (parametric plotting range).

• the use of the params dictionary to specify sliders in their basic form: (default, min, max).

from sympy import *
from spb import *
x, u, a, b = symbols("x, u, a, b")
graphics(
    contour_abs_arg(
        sqrt(x) * exp(u * x), prange(x, -3*a-b*3j, 3*a+b*3j),
        arg=False, use_cm=True,
        params={
            u: (0.25, 0, 1),
            a: (1, 0, 2),
            b: (1, 0, 2)
        }),
    grid=False)

(Source code, small.png)

spb.graphics.complex_analysis.surface_real_imag(expr, range=None, label=None, rendering_kw=None, real=True, imag=True, **kwargs)

Plot the real and imaginary part of a complex function f(x) with x in Complex.

Parameters:

exprExpr

Symbolic expression representing the function of one variable to be plotted.

range(symbol, min, max)

A 3-tuple denoting the range of the x variable. Default values: min=-10-10j and max=10+10j.

labelstr, optional

The label to be shown in the legend. If not provided, the string representation of expr will be used.

rendering_kwdict, optional

A dictionary of keywords/values which is passed to the backend’s function to customize the appearance of surfaces. Refer to the plotting library (backend) manual for more informations.

realboolean, optional

Show/hide the real part. Default to True (visible).

imagboolean, optional

Show/hide the imaginary part. Default to True (visible).

**kwargs

Keyword arguments are the same as surface(). Refer to its documentation for a for a full list of keyword arguments.

Returns:

serieslist

A list containing up two to instance of ComplexSurfaceSeries and possibly multiple instances of Parametric3DLineSeries, if wireframe=True.

See also

spb.graphics.functions_3d.surface, contour_abs_arg, contour_real_imag

surface_abs_arg

Examples

>>> from sympy import symbols, sqrt
>>> from spb import *
>>> x = symbols('x')

(Source code)

>>> graphics(
...     surface_real_imag(sqrt(x), (x, -3-3j, 3+3j), n=101))
Plot object containing:
[0]: complex cartesian surface: re(sqrt(x)) for re(x) over (-3.0, 3.0) and im(x) over (-3.0, 3.0)
[1]: complex cartesian surface: im(sqrt(x)) for re(x) over (-3.0, 3.0) and im(x) over (-3.0, 3.0)

(Source code, png)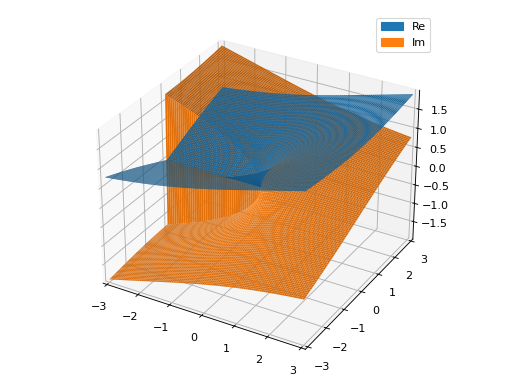

Interactive-widget plot. Refer to the interactive sub-module documentation to learn more about the params dictionary. This plot illustrates:

• the use of prange (parametric plotting range).

• the use of the params dictionary to specify sliders in their basic form: (default, min, max).

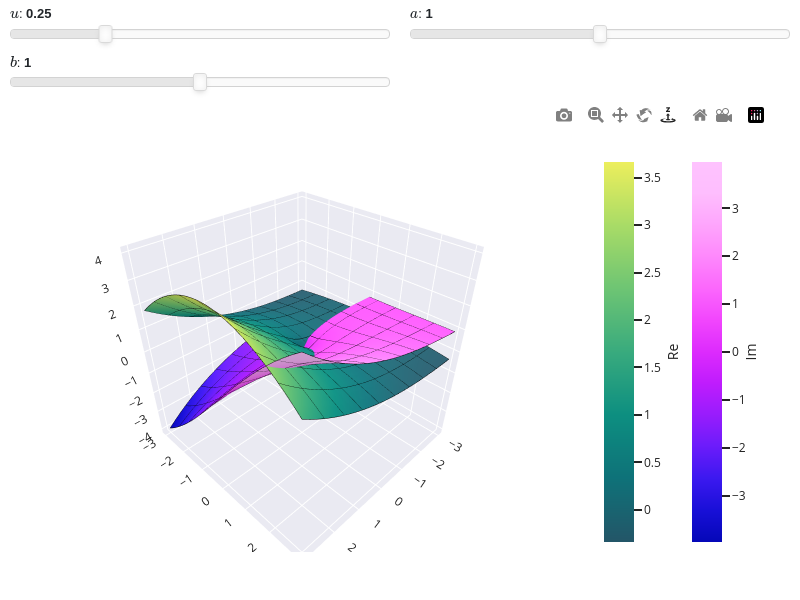
from sympy import *
from spb import *
x, u, a, b = symbols("x, u, a, b")
graphics(
    surface_real_imag(
        sqrt(x) * exp(u * x), prange(x, -3*a-b*3j, 3*a+b*3j),
        n=25, wireframe=True, wf_rendering_kw={"line_width": 1},
        use_cm=True, params={
            u: (0.25, 0, 1),
            a: (1, 0, 2),
            b: (1, 0, 2)
        }),
        backend=PB, aspect="cube")

(Source code, small.png)

spb.graphics.complex_analysis.contour_real_imag(expr, range=None, label=None, rendering_kw=None, real=True, imag=True, **kwargs)

Plot contours of the real and imaginary parts of a complex function f(x) with x in Complex.

Parameters:

exprExpr

Symbolic expression representing the function of one variable to be plotted.

range(symbol, min, max)

A 3-tuple denoting the range of the x variable. Default values: min=-10-10j and max=10+10j.

labelstr, optional

The label to be shown in the legend. If not provided, the string representation of expr will be used.

rendering_kwdict, optional

A dictionary of keywords/values which is passed to the backend’s function to customize the appearance of contours. Refer to the plotting library (backend) manual for more informations.

realboolean, optional

Show/hide the real part. Default to True (visible).

argboolean, optional

Show/hide the imaginary part. Default to True (visible).

**kwargs

Keyword arguments are the same as contour(). Refer to its documentation for a for a full list of keyword arguments.

Returns:

serieslist

A list containing up two to instance of ComplexSurfaceSeries.

See also

spb.graphics.functions_2d.contour, contour_abs_arg, surface_real_imag

surface_abs_arg

Examples

>>> from sympy import symbols, sqrt
>>> from spb import *
>>> x = symbols('x')

(Source code)

>>> graphics(
...     contour_real_imag(sqrt(x), (x, -3-3j, 3+3j), imag=False),
...     grid=False)
Plot object containing:
[0]: complex contour: re(sqrt(x)) for re(x) over (-3.0, 3.0) and im(x) over (-3.0, 3.0)

(Source code, png)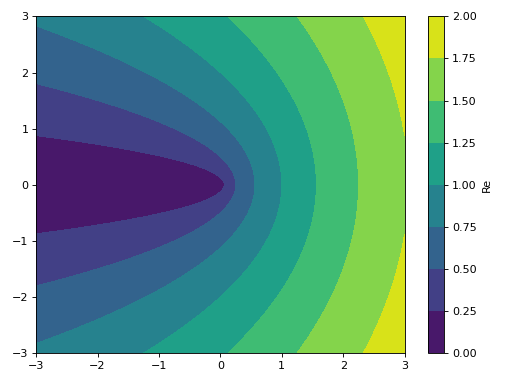

Interactive-widget plot. Refer to the interactive sub-module documentation to learn more about the params dictionary. This plot illustrates:

• the use of prange (parametric plotting range).

• the use of the params dictionary to specify sliders in their basic form: (default, min, max).

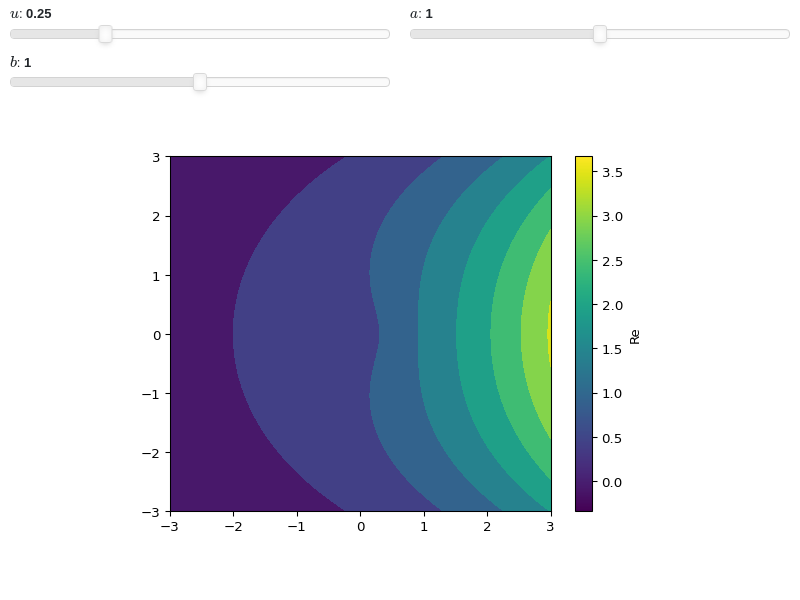
from sympy import *
from spb import *
x, u, a, b = symbols("x, u, a, b")
graphics(
    contour_real_imag(
        sqrt(x) * exp(u * x), prange(x, -3*a-b*3j, 3*a+b*3j),
        imag=False, use_cm=True,
        params={
            u: (0.25, 0, 1),
            a: (1, 0, 2),
            b: (1, 0, 2)
        }),
    grid=False)

(Source code, small.png)

spb.graphics.complex_analysis.domain_coloring(expr, range=None, label=None, rendering_kw=None, coloring=None, cmap=None, phaseres=20, phaseoffset=0, blevel=0.75, colorbar=True, **kwargs)

Plot an image of the absolute value of a complex function f(x) colored by its argument, with x in Complex.

Parameters:

exprExpr

Symbolic expression representing the function of one variable to be plotted.

range(symbol, min, max)

A 3-tuple denoting the range of the x variable. Default values: min=-10-10j and max=10+10j.

labelstr, optional

The label to be shown in the legend. If not provided, the string representation of expr will be used.

rendering_kwdict, optional

A dictionary of keywords/values which is passed to the backend’s function to customize the appearance of the image. Refer to the plotting library (backend) manual for more informations.

blevelfloat, optional

Controls the black level of ehanced domain coloring plots. It must be 0 (black) <= blevel <= 1 (white). Default to 0.75.

cmapstr, iterable, optional

Specify the colormap to be used on enhanced domain coloring plots (both images and 3d plots). Default to "hsv". Can be any colormap from matplotlib or colorcet.

colorbarboolean, optional

Show/hide the colorbar. Default to True (colorbar is visible).

coloringstr or callable, optional

Choose between different domain coloring options. Default to "a". Refer to [Wegert] for more information.

• "a": standard domain coloring showing the argument of the complex function.

• "b": enhanced domain coloring showing iso-modulus and iso-phase lines.

• "c": enhanced domain coloring showing iso-modulus lines.

• "d": enhanced domain coloring showing iso-phase lines.

• "e": alternating black and white stripes corresponding to modulus.

• "f": alternating black and white stripes corresponding to phase.

• "g": alternating black and white stripes corresponding to real part.

• "h": alternating black and white stripes corresponding to imaginary part.

• "i": cartesian chessboard on the complex points space. The result will hide zeros.

• "j": polar Chessboard on the complex points space. The result will show conformality.

• "k": black and white magnitude of the complex function. Zeros are black, poles are white.

• "k+log": same as "k" but apply a base 10 logarithm to the magnitude, which improves the visibility of zeros of functions with steep poles.

• "l":enhanced domain coloring showing iso-modulus and iso-phase lines, blended with the magnitude: white regions indicates greater magnitudes. Can be used to distinguish poles from zeros.

• "m": enhanced domain coloring showing iso-modulus lines, blended with the magnitude: white regions indicates greater magnitudes. Can be used to distinguish poles from zeros.

• "n": enhanced domain coloring showing iso-phase lines, blended with the magnitude: white regions indicates greater magnitudes. Can be used to distinguish poles from zeros.

• "o": enhanced domain coloring showing iso-phase lines, blended with the magnitude: white regions indicates greater magnitudes. Can be used to distinguish poles from zeros.

The user can also provide a callable, f(w), where w is an [n x m] Numpy array (provided by the plotting module) containing the results (complex numbers) of the evaluation of the complex function. The callable should return:

• imgndarray [n x m x 3]

  An array of RGB colors (0 <= R,G,B <= 255)

• colorscalendarray [N x 3] or None

  An array with N RGB colors, (0 <= R,G,B <= 255). If colorscale=None, no color bar will be shown on the plot.

n, n1, n2int, optional

Number of discretization points in the horizontal and vertical directions. Default to 300. n is a shortcut to set the same number of discretization points on both directions.

phaseresint, optional

Default value to 20. It controls the number of iso-phase and/or iso-modulus lines in domain coloring plots.

phaseoffsetfloat, optional

Controls the phase offset of the colormap in domain coloring plots. Default to 0.

paramsdict, optional

A dictionary mapping symbols to parameters. This keyword argument enables the interactive-widgets plot. Learn more by reading the documentation of the interactive sub-module.

Returns:

serieslist

A list containing an instance of ComplexDomainColoringSeries.

See also

analytic_landscape, riemann_sphere_2d

Notes

By default, a domain coloring plot will show the phase portrait: each point of the complex plane is color-coded according to its argument. The default colormap is HSV, which is characterized by 2 important problems:

• It is not friendly to people affected by color deficiencies.

• It might be misleading because it isn’t perceptually uniform: features disappear at points of low perceptual contrast, or false features appear that are in the colormap but not in the data (refer to [colorcet] for more information).

Hence, it might be helpful to chose a perceptually uniform colormap. Domaing coloring plots are naturally suited to be represented by cyclic colormaps, but sequential colormaps can be used too. In the following example we illustrate the phase portrait of f(z) = z using different colormaps:

from sympy import symbols, pi
import colorcet
from spb import *

z = symbols("z")
cmaps = {
    "hsv": "hsv",
    "twilight": "twilight",
    "colorwheel": colorcet.colorwheel,
    "CET-C7": colorcet.CET_C7,
    "viridis": "viridis"
}
plots = []
for k, v in cmaps.items():
    plots.append(
        graphics(domain_coloring(z, (z, -2-2j, 2+2j), coloring="a",
            cmap=v),
        grid=False, show=False, legend=True, title=k))

plotgrid(*plots, nc=2, size=(6.5, 8))

(Source code, png)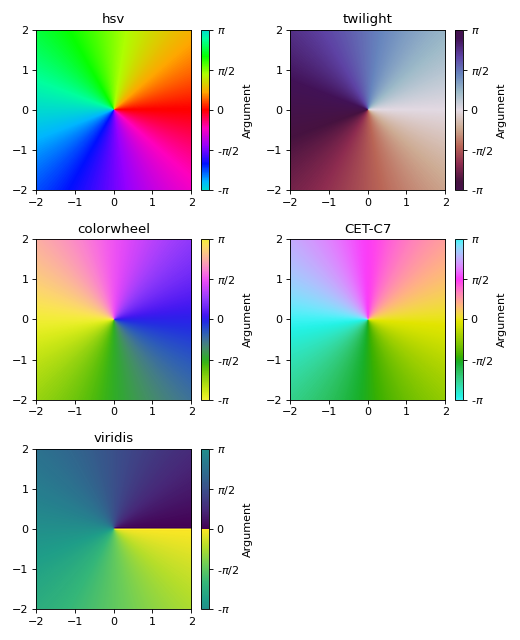

In the above figure, when using the HSV colormap the eye is drawn to the yellow, cyan and magenta colors, where there is a lightness gradient: those are false features caused by the colormap. Indeed, there is nothing going on these regions when looking with a perceptually uniform colormap.

Phase is computed with Numpy and lies between [-pi, pi]. Then, phase is normalized between [0, 1] using (arg / (2 * pi)) % 1. The figure below shows the mapping between phase in radians and normalized phase. A phase of 0 radians corresponds to a normalized phase of 0, which gets mapped to the beginning of a colormap.

(Source code, png)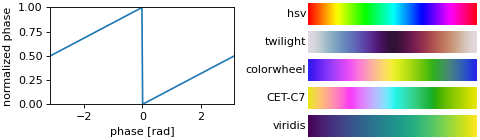

The zero radians phase is then located in the middle of the colorbar. Hence, the colorbar might feel “weird” if a sequential colormap is chosen, because there is a color-discontinuity in the middle of it, as can be seen in the previous example. The phaseoffset keyword argument allows to adjust the position of the colormap:

p1 = graphics(
    domain_coloring(z, (z, -2-2j, 2+2j), coloring="a",
        cmap="viridis", phaseoffset=0),
    grid=False, show=False, legend=True, aspect="equal",
    title="phase offset = 0", axis=False)
p2 = graphics(
    domain_coloring(z, (z, -2-2j, 2+2j), coloring="a",
        cmap="viridis", phaseoffset=pi),
    grid=False, show=False, legend=True, aspect="equal",
    title=r"phase offset = $\pi$", axis=False)
plotgrid(p1, p2, nc=2, size=(6, 2))

(Source code, png)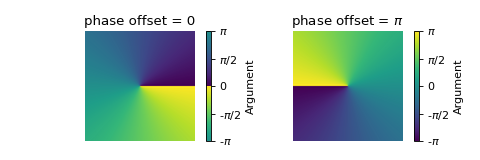

A pure phase portrait is rarely useful, as it conveys too little information. Let’s now quickly visualize the different coloring schemes. In the following, arg is the argument (phase), mag is the magnitude (absolute value) and contour is a line of constant value. Refer to [Wegert] for more information.

from matplotlib import rcParams
rcParams["font.size"] = 8
colorings = "abcdlmnoefghijk"
titles = [
    "phase portrait", "mag + arg contours", "mag contours", "arg contours",
    "'a' + poles", "'b' + poles", "'c' + poles", "'d' + poles",
    "mag stripes", "arg stripes", "real part stripes", "imag part stripes",
    "hide zeros", "conformality", "magnitude"]
plots = []
expr = (z - 1) / (z**2 + z + 1)
for c, t in zip(colorings, titles):
    plots.append(
        graphics(domain_coloring(expr, (z, -2-2j, 2+2j), coloring=c,
            cmap=colorcet.CET_C2, colorbar=False),
        grid=False, show=False, legend=False, axis=False,
        title=("'%s'" % c) + ": " + t, xlabel="", ylabel=""))

plotgrid(*plots, nc=4, size=(8, 8.5))

(Source code, png)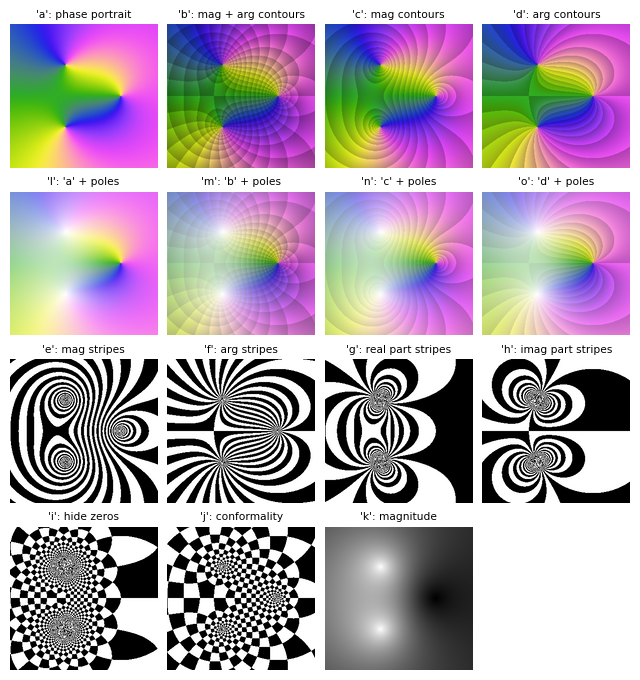

From the above picture, we can see that:

• Some enhancements decrese the lighness of the colors: depending on the colormap, it might be difficult to distinguish features in darker regions.

• Other enhancements increases the lightness in proximity of poles. Hence, colormaps with very light colors might not convey enough information.

With these considerations in mind, the selection of a proper colormap is left to the user because not only it depends on the target audience of the visualization, but also on the function being visualized.

Examples

>>> from sympy import I, symbols, exp, sqrt, cos, sin, pi, gamma
>>> from spb import *
>>> x, y, z = symbols('x, y, z')

(Source code)

To improve the smoothness of the results, increase the number of discretization points and/or apply an interpolation (if the backend supports it):

>>> graphics(
...     domain_coloring(gamma(z), (z, -3-3j, 3+3j), coloring="b", n=500),
...     grid=False)
Plot object containing:
[0]: complex domain coloring: gamma(z) for re(z) over (-3.0, 3.0) and im(z) over (-3.0, 3.0)

(Source code, png)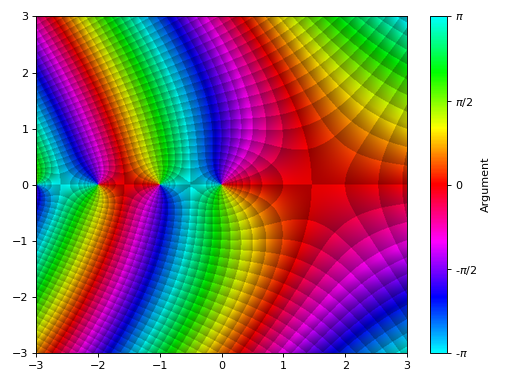

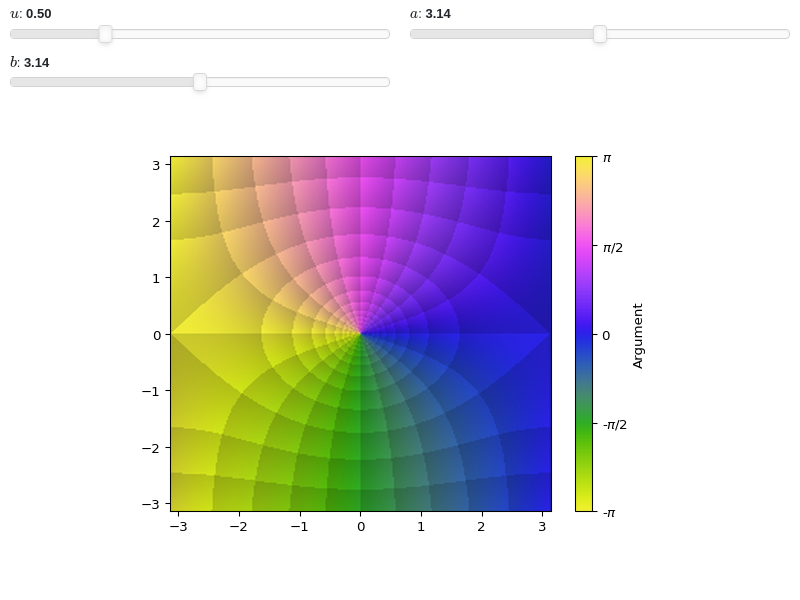
Interactive-widget domain coloring plot. Refer to the interactive sub-module documentation to learn more about the params dictionary. This plot illustrates:

• setting a custom colormap and adjusting the black-level of the enhanced visualization.

• the use of prange (parametric plotting range).

• the use of the params dictionary to specify sliders in their basic form: (default, min, max).

from sympy import *
from spb import *
import colorcet
z, u, a, b = symbols("z, u, a, b")
graphics(
    domain_coloring(sin(u * z), prange(z, -a - b*I, a + b*I),
        cmap=colorcet.colorwheel, blevel=0.85,
        coloring="b", n=250,
        params={
            u: (0.5, 0, 2),
            a: (pi, 0, 2*pi),
            b: (pi, 0, 2*pi),
        }),
    grid=False
)

(Source code, small.png)

spb.graphics.complex_analysis.analytic_landscape(expr, range=None, label=None, rendering_kw=None, **kwargs)

Plot a surface of the absolute value of a complex function f(x) colored by its argument, with x in Complex.

Parameters:

**kwargs

Keyword arguments are the same as domain_coloring(). Refer to its documentation for a for a full list of keyword arguments.

Returns:

serieslist

A list containing up two to instance of ComplexDomainColoringSeries.

See also

domain_coloring

Examples

from sympy import symbols, gamma, I
from spb import *
z = symbols('z')
graphics(
    analytic_landscape(gamma(z), (z, -3 - 3*I, 3 + 3*I)),
    backend=PB, zlim=(-1, 6))

(Source code, png)

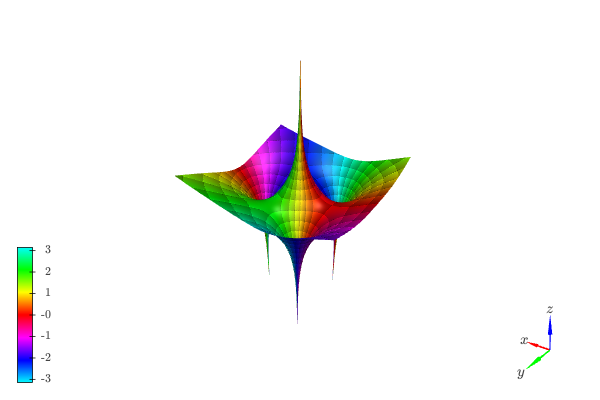
Because the function goes to infinity at poles, sometimes it might be beneficial to visualize the logarithm of the absolute value in order to easily identify zeros:

from sympy import symbols, I
from spb import *
import numpy as np
z = symbols("z")
expr = (z**3 - 5) / z
graphics(
    analytic_landscape(expr, (z, -3-3j, 3+3j), coloring="b", n=500,
        tz=np.log),
    grid=False, backend=KB)

(Source code, small.png)

spb.graphics.complex_analysis.riemann_sphere_2d(expr, range=None, label=None, rendering_kw=None, at_infinity=False, riemann_mask=True, annotate=True, **kwargs)

Visualize stereographic projections of the Riemann sphere.

Refer to plot_riemann_sphere() to learn more about the Riemann sphere.

Parameters:

exprExpr

Represent the complex function to be plotted.

range3-element tuple, optional

Denotes the range of the variables. Default to (z, -1.25 - 1.25*I, 1.25 + 1.25*I).

colorbarboolean, optional

Show/hide the colorbar. Default to True (colorbar is visible).

annotateboolean, optional

Turn on/off the annotations on the 2D projections of the Riemann sphere. Default to True (annotations are visible). They can only be visible when riemann_mask=True.

at_infinityboolean, optional

If True, the center of the visualization is placed at infinity. Otherwise, it is placed at zero. Default to False.

riemann_maskboolean, optional

Turn on/off the unit disk mask representing the Riemann sphere on the 2D projections. Default to True (mask is active).

**kwargs

Keyword arguments are the same as domain_coloring(). Refer to its documentation for a for a full list of keyword arguments.

Returns:

serieslist

A list containing up two to instance of ComplexDomainColoringSeries.

See also

riemann_sphere_3d, domain_coloring

spb.plot_functions.complex_analysis.plot_riemann_sphere

Notes

plot_riemann_sphere() returns a plotgrid() of two visualizations, one with at_infinity=True, the other with at_infinity=False. Read its documentation to learn more about the [Riemann-sphere].

Examples

Visualization centerd at zero:

>>> from sympy import I, symbols, exp, sqrt, cos, sin, pi, gamma
>>> from spb import *
>>> z = symbols("z")
>>> expr = (z - 1) / (z**2 + z + 2)
>>> graphics(riemann_sphere_2d(expr, coloring="b", n=800), grid=False)
Plot object containing:
[0]: complex domain coloring: (z - 1)/(z**2 + z + 2) for re(z) over (-1.25, 1.25) and im(z) over (-1.25, 1.25)
[1]: parametric cartesian line: (cos(t), sin(t)) for t over (0.0, 6.283185307179586)

(Source code, png)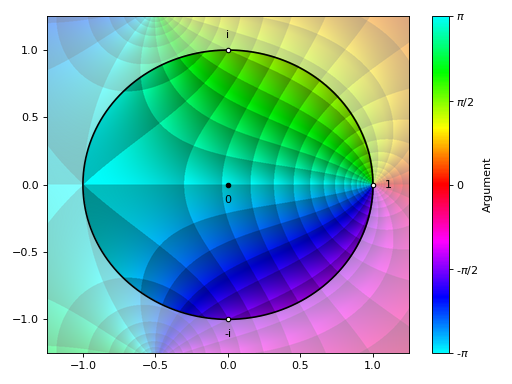

Visualization centerd at infinity:

>>> graphics(riemann_sphere_2d(expr, coloring="b", n=800,
...     at_infinity=True), grid=False)
Plot object containing:
[0]: complex domain coloring: (-1 + 1/z)/(2 + 1/z + z**(-2)) for re(z) over (-1.25, 1.25) and im(z) over (-1.25, 1.25)
[1]: parametric cartesian line: (cos(t), sin(t)) for t over (0.0, 6.283185307179586)

(Source code, png)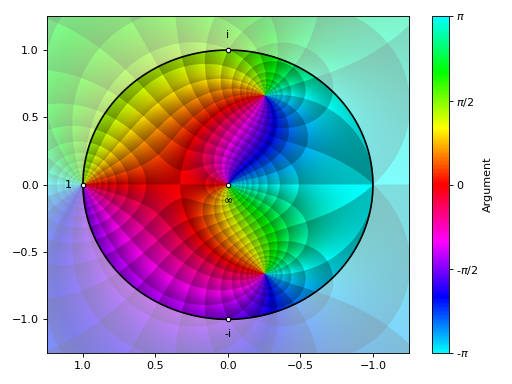

spb.graphics.complex_analysis.riemann_sphere_3d(expr, rendering_kw=None, colorbar=True, **kwargs)

Visualize a complex function over the Riemann sphere.

Parameters:

exprExpr

Represent the complex function to be plotted.

colorbarboolean, optional

Show/hide the colorbar. Default to True (colorbar is visible).

**kwargs

Keyword arguments are the same as analytic_landscape(). Refer to its documentation for a for a full list of keyword arguments.

Returns:

serieslist

A list containing two to instance of RiemannSphereSeries.

See also

riemann_sphere_2d, domain_coloring

Examples

from sympy import *
from spb import *
z = symbols("z")
expr = (z - 1) / (z**2 + z + 1)
graphics(
    riemann_sphere_3d(expr, n=150,
        coloring="b"),
    backend=KB, legend=False, grid=False)

(Source code, small.png)

spb.graphics.complex_analysis.complex_vector_field(expr, range=None, **kwargs)

Plot the vector field [re(f), im(f)] for a complex function f over the specified complex domain.

Parameters:

exprExpr

Represent the complex function.

range3-element tuples

Denotes the range of the variables. For example (z, -5 - 3*I, 5 + 3*I). Note that we can specify the range by using standard Python complex numbers, for example (z, -5-3j, 5+3j).

labelstr, optional

The name of the complex expression to be eventually shown on the legend. If none is provided, the string representation of the expression will be used.

**kwargs

Keyword arguments are the same as vector_field_2d(). Refer to its documentation for a for a full list of keyword arguments.

Returns:

serieslist

A list containing one instance of ContourSeries (if scalar is set) and one instance of Vector2DSeries.

See also

spb.graphics.vectors.vector_field_2d

Examples

>>> from sympy import I, symbols, gamma, latex, log
>>> from spb import *
>>> z = symbols('z')

(Source code)

Quivers plot with normalize lengths and a contour plot in background representing the vector’s magnitude (a scalar field).

>>> expr = z**2 + 2
>>> graphics(
...     complex_vector_field(expr,  (z, -5 - 5j, 5 + 5j),
...         quiver_kw=dict(color="orange"), normalize=True,
...         contour_kw={"levels": 20}),
...     grid=False)
Plot object containing:
[0]: contour: sqrt(4*(re(_x) - im(_y))**2*(re(_y) + im(_x))**2 + ((re(_x) - im(_y))**2 - (re(_y) + im(_x))**2 + 2)**2) for _x over (-5.0, 5.0) and _y over (-5.0, 5.0)
[1]: 2D vector series: [(re(_x) - im(_y))**2 - (re(_y) + im(_x))**2 + 2, 2*(re(_x) - im(_y))*(re(_y) + im(_x))] over (_x, -5.0, 5.0), (_y, -5.0, 5.0)

(Source code, png)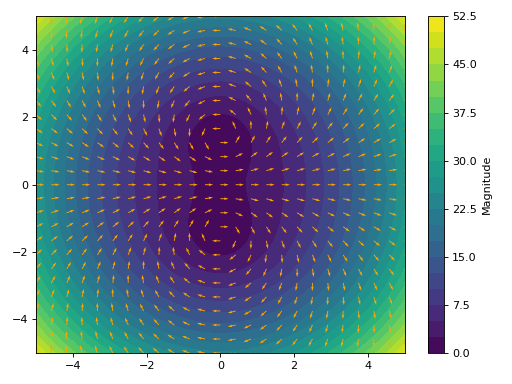

Only quiver plot with normalized lengths and solid color.

>>> graphics(
...     complex_vector_field(expr,  (z, -5 - 5j, 5 + 5j),
...         scalar=False, use_cm=False, normalize=True),
...     grid=False, aspect="equal")
Plot object containing:
[0]: 2D vector series: [(re(_x) - im(_y))**2 - (re(_y) + im(_x))**2 + 2, 2*(re(_x) - im(_y))*(re(_y) + im(_x))] over (_x, -5.0, 5.0), (_y, -5.0, 5.0)

(Source code, png)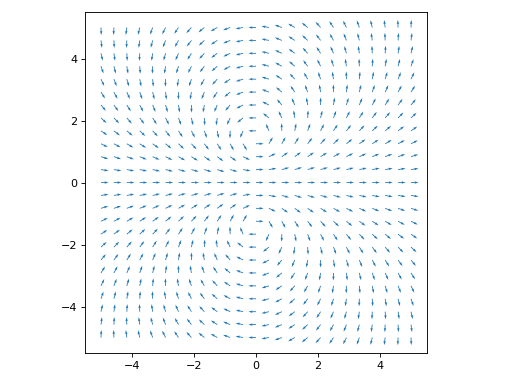

Only streamlines plot.

>>> graphics(
...     complex_vector_field(expr, (z, -5 - 5j, 5 + 5j),
...         label="Magnitude of $%s$" % latex(expr),
...         scalar=False, streamlines=True))
Plot object containing:
[0]: 2D vector series: [(re(_x) - im(_y))**2 - (re(_y) + im(_x))**2 + 2, 2*(re(_x) - im(_y))*(re(_y) + im(_x))] over (_x, -5.0, 5.0), (_y, -5.0, 5.0)

(Source code, png)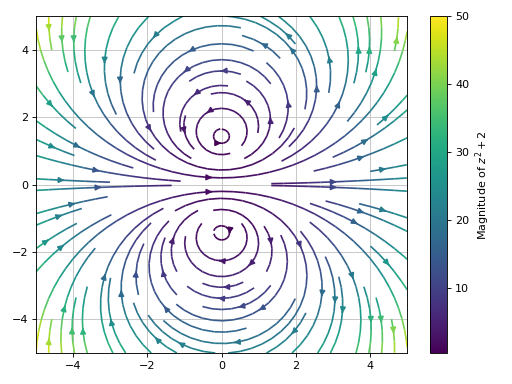

Overlay the quiver plot to a domain coloring plot. By setting n=26 (even number) in the complex vector plot, the quivers won’t to cross the branch cut.

>>> expr = z * log(2 * z) + 3
>>> graphics(
...     domain_coloring(expr, (z, -2-2j, 2+2j)),
...     complex_vector_field(expr, (z, -2-2j, 2+2j),
...         n=26, scalar=False, use_cm=False, normalize=True,
...         show_in_legend=False,
...         quiver_kw={"color": "k", "pivot": "tip"}),
...     grid=False)
Plot object containing:
[0]: complex domain coloring: z*log(2*z) + 3 for re(z) over (-2.0, 2.0) and im(z) over (-2.0, 2.0)
[1]: 2D vector series: [(re(_x) - im(_y))*log(Abs(2*_x + 2*_y*I)) - (re(_y) + im(_x))*arg(_x + _y*I) + 3, (re(_x) - im(_y))*arg(_x + _y*I) + (re(_y) + im(_x))*log(Abs(2*_x + 2*_y*I))] over (_x, -2.0, 2.0), (_y, -2.0, 2.0)

(Source code, png)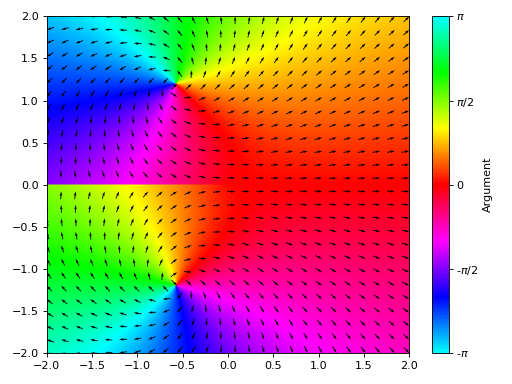

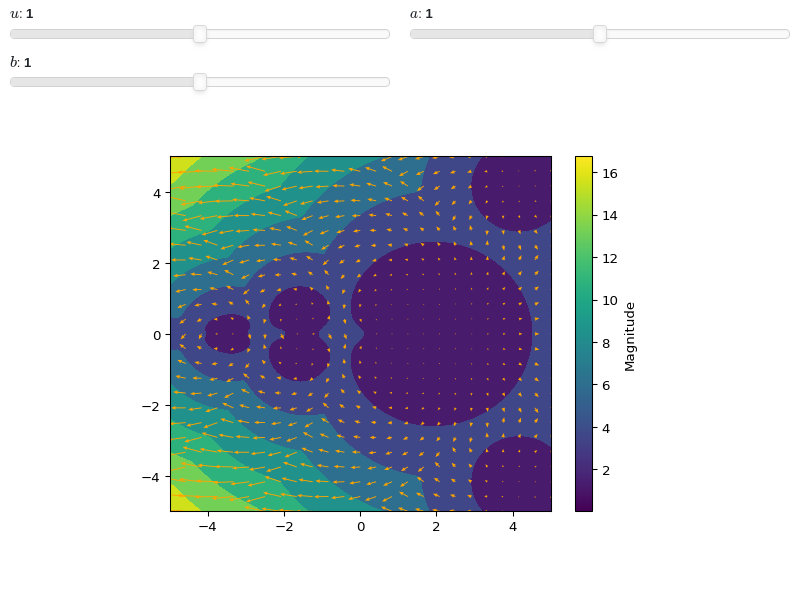
Interactive-widget plot. Refer to the interactive sub-module documentation to learn more about the params dictionary. This plot illustrates:

• the use of prange (parametric plotting range).

• the use of the params dictionary to specify sliders in their basic form: (default, min, max).

from sympy import *
from spb import *
z, u, a, b = symbols("z u a b")
graphics(
    complex_vector_field(
        log(gamma(u * z)), prange(z, -5*a - b*5j, 5*a + b*5j),
        params={
            u: (1, 0, 2),
            a: (1, 0, 2),
            b: (1, 0, 2)
        }, quiver_kw=dict(color="orange", headwidth=4)),
    n=20, grid=False)

(Source code, small.png)