2D general plotting

NOTE: For technical reasons, all interactive-widgets plots in this documentation are created using Holoviz’s Panel. Often, they will ran just fine with ipywidgets too. However, if a specific example uses the param library, or widgets from the panel module, then users will have to modify the params dictionary in order to make it work with ipywidgets. Refer to Interactive module for more information.

spb.graphics.functions_2d.line(expr, range_x=None, label=None, rendering_kw=None, **kwargs)[source]

Plot a function of one variable over a 2D space.

Parameters:
expr

It can either be a symbolic expression representing the function of one variable to be plotted, or a numerical function of one variable, supporting vectorization. In the latter case the following keyword arguments are not supported: params, sum_bound.

range_xtuple, Tuple

A 3-tuple (symb, min, max) denoting the range of the x variable. Default values: min=-10 and max=10.

labelstr

Set the label associated to this series, which will be eventually shown on the legend or colorbar.

rendering_kwdict

A dictionary of keyword arguments to be passed to the renderers in order to further customize the appearance of the line. Here are some useful links for the supported plotting libraries:

color_func

A color function to be applied to the numerical data. It can be:

  • A numerical function of 2 variables, x, y (the points computed by the internal algorithm) supporting vectorization.

  • A symbolic expression having at most as many free symbols as expr.

  • None: the default value (no color mapping).

colorbarbool

Toggle the visibility of the colorbar associated to the current data series. Note that a colorbar is only visible if use_cm=True and color_func is not None. Default value: True.

colorbar_ticks_formattertick_formatter_multiples_of

An object of type tick_formatter_multiples_of which will be used to place tick values on the colorbar at each multiple of a specified quantity. This only works when use_cm=True.

detect_polesbool, str

Chose whether to detect and correctly plot the roots of the denominator. There are two algorithms at work:

  1. based on the gradient of the numerical data, it introduces NaN values at locations where the steepness is greater than some threshold. This splits the line into multiple segments. To improve detection, increase the number of discretization points n and/or change the value of eps. This algorithm can be used to visualize jump discontinuities as well as essential discontinuities.

  2. a symbolic approach based on the continuous_domain function from the sympy.calculus.util module, which computes the locations of essential discontinuities. If any are found, vertical lines will be shown.

Possible options:

  • False: No poles detection

  • True: Poles detection with the numerical algorithm

  • ‘symbolic’: Poles detection with numerical and symbolic algorithms

Default value: False.

epsfloat

An arbitrary small value used by the detect_poles numerical algorithm. Before changing this value, it is recommended to increase the number of discretization points. Related parameters: detect_poles. It must be: 0 ≤ eps < ∞. Default value: 0.01.

excludelist

List of x-coordinates to be excluded from evaluation. In practice, it introduces discontinuities in the resulting line.

force_real_evalbool

By default, numerical evaluation is performed over complex numbers, which is slower but produces correct results. However, when the symbolic expression is converted to a numerical function with lambdify, the resulting function may not like to be evaluated over complex numbers. In such cases, forcing the evaluation to be performed over real numbers might be a good choice. The plotting module should be able to detect such occurences and automatically activate this option. If that is not the case, or evaluation performance is of paramount importance, set this parameter to True, but be aware that it might produce wrong results. Default value: False.

is_filledbool

Whether scatter’s markers are filled or void. Default value: True.

is_scatterbool

If True it represent a scatter plot, otherwise a continuous line. Default value: False.

line_color

For back-compatibility with old sympy.plotting. Use rendering_kw in order to fully customize the appearance of the line/scatter.

modules

Specify the evaluation modules to be used by lambdify. If not specified, the evaluation will be done with NumPy/SciPy.

n1int

Number of discretization points along the parameter to be used in the numerical evaluation. An alias of this parameter is n. Related parameters: xscale. It must be: 2 ≤ n1 < ∞. Default value: 1000.

only_integersbool

Discretize the domain using only integer numbers. When this parameter is True, the number of discretization points is choosen by the algorithm. Default value: False.

paramsdict, optional

A dictionary mapping symbols to parameters. If provided, this dictionary enables the interactive-widgets plot.

When calling a plotting function, the parameter can be specified with:

  • a widget from the ipywidgets module.

  • a widget from the panel module.

  • a tuple of the form:

    (default, min, max, N, tick_format, label, spacing), which will instantiate a ipywidgets.widgets.widget_float.FloatSlider or a ipywidgets.widgets.widget_float.FloatLogSlider, depending on the spacing strategy. In particular:

    • default, min, maxfloat

      Default value, minimum value and maximum value of the slider, respectively. Must be finite numbers. The order of these 3 numbers is not important: the module will figure it out which is what.

    • Nint, optional

      Number of steps of the slider.

    • tick_formatstr or None, optional

      Provide a formatter for the tick value of the slider. Default to ".2f".

    • label: str, optional

      Custom text associated to the slider.

    • spacingstr, optional

      Specify the discretization spacing. Default to "linear", can be changed to "log".

Notes:

  1. parameters cannot be linked together (ie, one parameter cannot depend on another one).

  2. If a widget returns multiple numerical values (like panel.widgets.slider.RangeSlider or ipywidgets.widgets.widget_float.FloatRangeSlider), then a corresponding number of symbols must be provided.

Here follows a couple of examples. If imodule="panel":

import panel as pn
params = {
    a: (1, 0, 5), # slider from 0 to 5, with default value of 1
    b: pn.widgets.FloatSlider(value=1, start=0, end=5), # same slider as above
    (c, d): pn.widgets.RangeSlider(value=(-1, 1), start=-3, end=3, step=0.1)
}

Or with imodule="ipywidgets":

import ipywidgets as w
params = {
    a: (1, 0, 5), # slider from 0 to 5, with default value of 1
    b: w.FloatSlider(value=1, min=0, max=5), # same slider as above
    (c, d): w.FloatRangeSlider(value=(-1, 1), min=-3, max=3, step=0.1)
}

When instantiating a data series directly, params must be a dictionary mapping symbols to numerical values.

Let series be any data series. Then series.params returns a dictionary mapping symbols to numerical values.

poles_locationslist

When detect_poles="symbolic", stores the location of the computed poles (essential discontinuities) so that they can be appropriately rendered.

poles_rendering_kwdict

Rendering kw used to customize the appearance of vertical lines representing essential discontinuities. Related parameters: poles_locations.

show_in_legendbool

Toggle the visibility of the data series on the legend. Default value: True.

stepsNoneType, bool, str

If set, it connects consecutive points with steps rather than straight segments. Possible options: [‘pre’, ‘post’, ‘mid’, True, False, None] Default value: False.

sum_boundint

When plotting sums, the expression will be pre-processed in order to replace lower/upper bounds set to +/- infinity with this +/- numerical value. Note: the higher this number, the slower the evaluation, but the more accurate the plot. It must be: 0 ≤ sum_bound < ∞. Default value: 1000.

txcallable

Numerical transformation function to be applied to the data on the x-axis.

tycallable

Numerical transformation function to be applied to the data on the y-axis.

unwrapbool, dict

Whether to use numpy.unwrap() on the computed coordinates in order to get rid of discontinuities. It can be:

  • False: do not use np.unwrap().

  • True: use np.unwrap() with default keyword arguments.

  • dictionary of keyword arguments passed to np.unwrap().

use_cmbool

Toggle the use of a colormap. By default, some series might use a colormap to display the necessary data. Setting this attribute to False will inform the associated renderer to use solid color. Related parameters: color_func. Default value: False.

xscalestr

Discretization strategy along the x-direction. Related parameters: n1. Possible options: [‘linear’, ‘log’] Default value: ‘linear’.

Returns:
serieslist

A list containing one instance of LineOver1DRangeSeries.

See also

line_parametric_2d, line_polar, implicit_2d, list_2d, geometry
spb.graphics.functions_3d.line_parametric_3d

Examples

>>> from sympy import symbols, sin, pi, tan, exp, cos, log, floor
>>> from spb import *
>>> x, y = symbols('x, y')

(Source code)

Single Plot

>>> graphics(line(x**2, (x, -5, 5)))
Plot object containing:
[0]: cartesian line: x**2 for x over (-5, 5)

(Source code, png)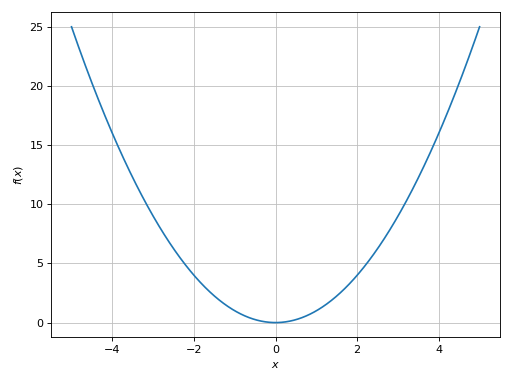

../../_images/functions_2d-2.png

Multiple functions over the same range with custom rendering options:

>>> graphics(
...     line(x, (x, -3, 3)),
...     line(log(x), (x, -3, 3), rendering_kw={"linestyle": "--"}),
...     line(exp(x), (x, -3, 3), rendering_kw={"linestyle": ":"}),
...     aspect="equal", ylim=(-3, 3)
... )
Plot object containing:
[0]: cartesian line: x for x over (-3, 3)
[1]: cartesian line: log(x) for x over (-3, 3)
[2]: cartesian line: exp(x) for x over (-3, 3)

(Source code, png)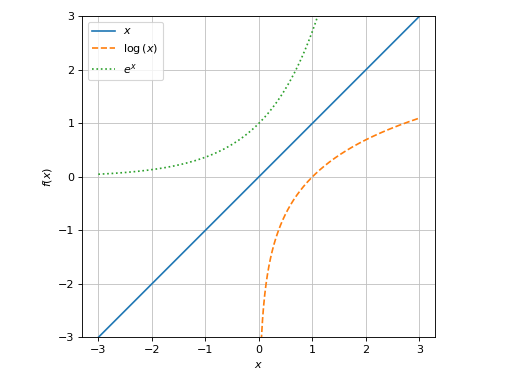

../../_images/functions_2d-3.png

Plotting a summation in which the free symbol of the expression is not used in the lower/upper bounds:

>>> from sympy import Sum, oo, latex
>>> expr = Sum(1 / x ** y, (x, 1, oo))
>>> graphics(
...     line(expr, (y, 2, 10), sum_bound=1e03),
...     title="$%s$" % latex(expr)
... )
Plot object containing:
[0]: cartesian line: Sum(x**(-y), (x, 1, oo)) for y over (2, 10)

(Source code, png)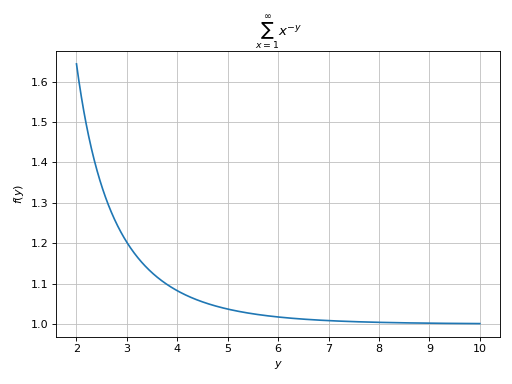

../../_images/functions_2d-4.png

Plotting a summation in which the free symbol of the expression is used in the lower/upper bounds. Here, the discretization variable must assume integer values:

>>> expr = Sum(1 / x, (x, 1, y))
>>> graphics(
...     line(expr, (y, 2, 10), is_scatter=True),
...     title="$%s$" % latex(expr)
... )
Plot object containing:
[0]: cartesian line: Sum(1/x, (x, 1, y)) for y over (2, 10)

(Source code, png)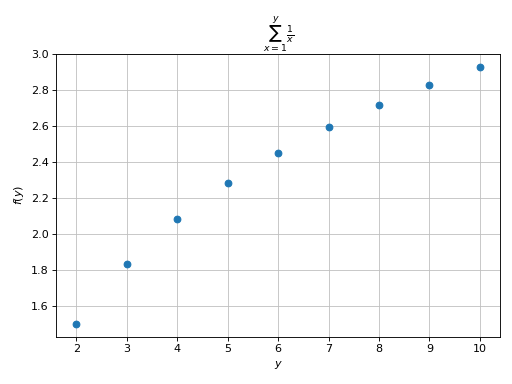

../../_images/functions_2d-5.png

Detect essential singularities and visualize them with vertical lines. Also, apply a tick formatter on the x-axis is order to show ticks at multiples of pi/2:

>>> import numpy as np
>>> graphics(
...     line(tan(x), (x, -1.5*pi, 1.5*pi), detect_poles="symbolic"),
...     x_ticks_formatter=multiples_of_pi_over_2(),
...     ylim=(-7, 7), xlabel="x [deg]", grid=False
... )
Plot object containing:
[0]: cartesian line: tan(x) for x over (-1.5*pi, 1.5*pi)

(Source code, png)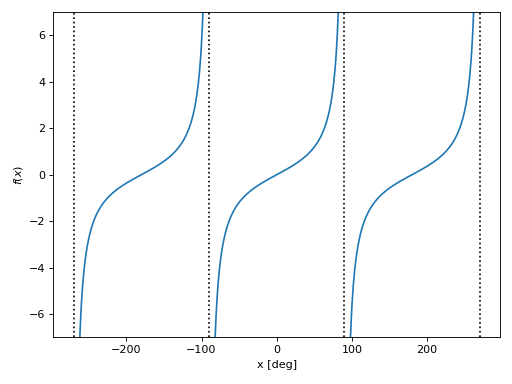

../../_images/functions_2d-6.png

Introducing discontinuities by excluding specified points:

>>> graphics(
...     line(floor(x) / x, (x, -3.25, 3.25), exclude=list(range(-4, 5))),
...     ylim=(-1, 5)
... )
Plot object containing:
[0]: cartesian line: floor(x)/x for x over (-3.25000000000000, 3.25000000000000)

(Source code, png)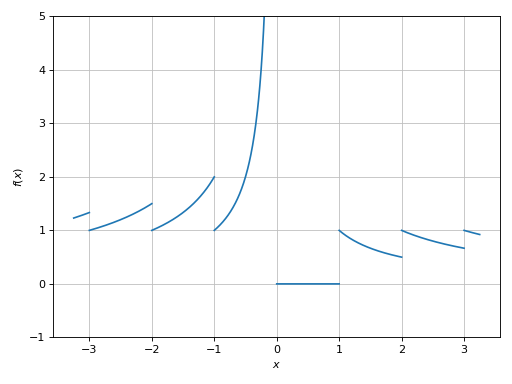

../../_images/functions_2d-7.png

Creating a step plot:

>>> graphics(
...     line(x-2, (x, 0, 10), only_integers=True, steps="pre", label="pre"),
...     line(x, (x, 0, 10), only_integers=True, steps="mid", label="mid"),
...     line(x+2, (x, 0, 10), only_integers=True, steps="post", label="post"),
... )
Plot object containing:
[0]: cartesian line: x - 2 for x over (0, 10)
[1]: cartesian line: x for x over (0, 10)
[2]: cartesian line: x + 2 for x over (0, 10)

(Source code, png)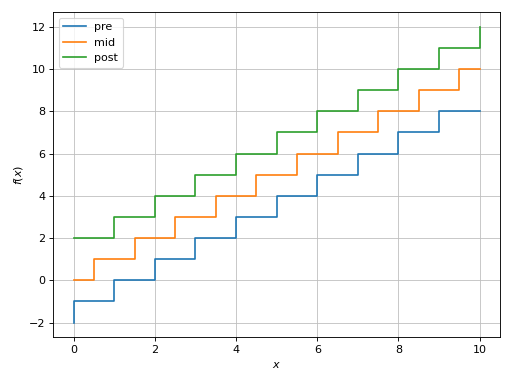

../../_images/functions_2d-8.png

Advanced example showing:

  • detect singularities by setting adaptive=False (better performance), increasing the number of discretization points (in order to have ‘vertical’ segments on the lines) and reducing the threshold for the singularity-detection algorithm.

  • application of color function.

  • combining together multiple lines.

>>> import numpy as np
>>> expr = 1 / cos(10 * x) + 5 * sin(x)
>>> def cf(x, y):
...     # map a colormap to the distance from the origin
...     d = np.sqrt(x**2 + y**2)
...     # visibility of the plot is limited: ylim=(-10, 10). However,
...     # some of the y-values computed by the function are much higher
...     # (or lower). Filter them out in order to have the entire
...     # colormap spectrum visible in the plot.
...     offset = 12 # 12 > 10 (safety margin)
...     d[(y > offset) | (y < -offset)] = 0
...     return d
>>> graphics(
...     line(
...         expr, (x, -5, 5), "distance from (0, 0)",
...         rendering_kw={"cmap": "plasma"},
...         adaptive=False, detect_poles=True, n=3e04,
...         eps=1e-04, color_func=cf),
...     line(5 * sin(x), (x, -5, 5), rendering_kw={"linestyle": "--"}),
...     ylim=(-10, 10), title="$%s$" % latex(expr)
... )
Plot object containing:
[0]: cartesian line: 5*sin(x) + 1/cos(10*x) for x over (-5, 5)
[1]: cartesian line: 5*sin(x) for x over (-5, 5)

(Source code, png)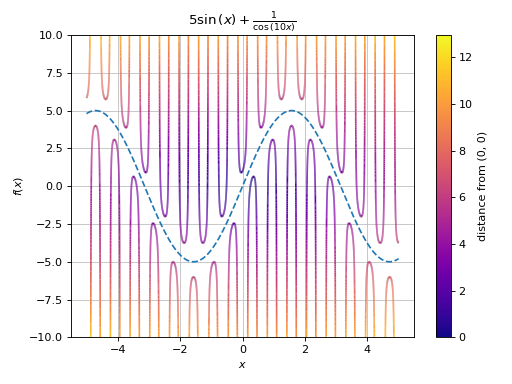

../../_images/functions_2d-9.png

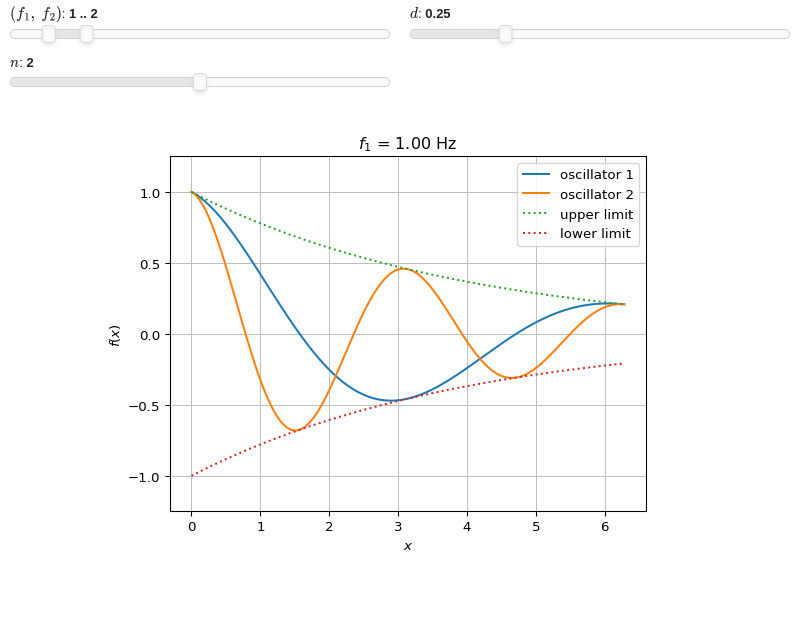
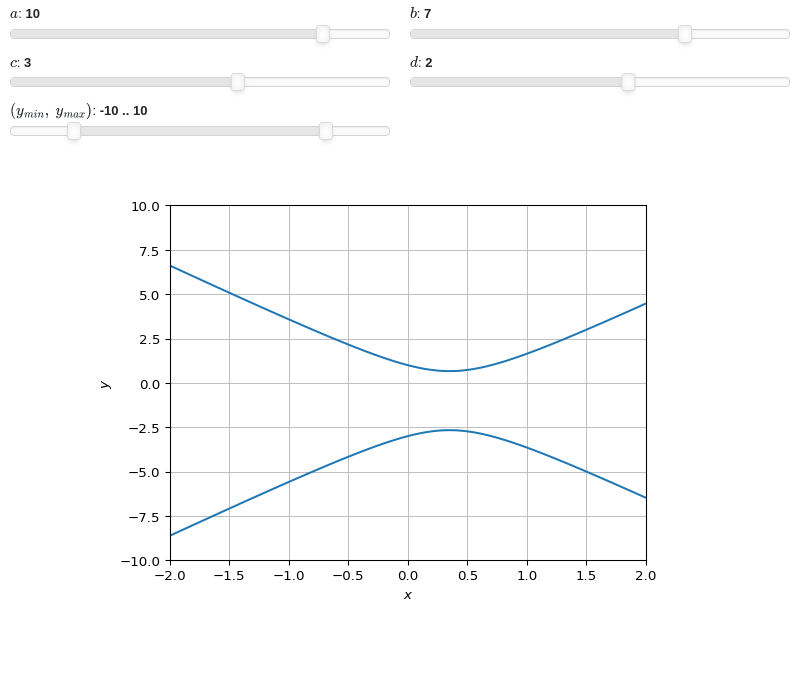
Interactive-widget plot of an oscillator. Refer to the interactive sub-module documentation to learn more about the params dictionary. This plot illustrates:

  • plotting multiple expressions, each one with its own label and rendering options.

  • the use of prange (parametric plotting range).

  • the use of the params dictionary to specify sliders in their basic form: (default, min, max).

  • the use of panel.widgets.slider.RangeSlider, which is a 2-values widget. In this case it is used to enforce the condition f1 < f2.

  • the use of a parametric title, specified with a tuple of the form: (title_str, param_symbol1, ...), where:

    • title_str must be a formatted string, for example: "test = {:.2f}".

    • param_symbol1, ... must be a symbol or a symbolic expression whose free symbols are contained in the params dictionary.

from sympy import *
from spb import *
import panel as pn
x, y, f1, f2, d, n = symbols("x, y, f_1, f_2, d, n")
params = {
    (f1, f2): pn.widgets.RangeSlider(
        value=(1, 2), start=0, end=10, step=0.1),     # frequencies
    d: (0.25, 0, 1),   # damping
    n: (2, 0, 4)       # multiple of pi
}
graphics(
    line(cos(f1 * x) * exp(-d * x), prange(x, 0, n * pi),
        label="oscillator 1", params=params),
    line(cos(f2 * x) * exp(-d * x), prange(x, 0, n * pi),
        label="oscillator 2", params=params),
    line(exp(-d * x), prange(x, 0, n * pi), label="upper limit",
        rendering_kw={"linestyle": ":"}, params=params),
    line(-exp(-d * x), prange(x, 0, n * pi), label="lower limit",
        rendering_kw={"linestyle": ":"}, params=params),
    ylim=(-1.25, 1.25),
    title=("$f_1$ = {:.2f} Hz", f1)
)

(Source code, small.png)

../../_images/functions_2d-10.small.png
spb.graphics.functions_2d.line_parametric_2d(expr_x, expr_y, range_p=None, label=None, rendering_kw=None, colorbar=True, use_cm=True, **kwargs)[source]

Plots a 2D parametric curve.

Parameters:
expr_x

The expression representing the component along the x-axis of the parametric function. It can either be a symbolic expression representing the function of one variable to be plotted, or a numerical function of one variable, supporting vectorization. In the latter case the following keyword arguments are not supported: params, sum_bound.

expr_y

The expression representing the component along the y-axis of the parametric function. It can either be a symbolic expression representing the function of one variable to be plotted, or a numerical function of one variable, supporting vectorization. In the latter case the following keyword arguments are not supported: params, sum_bound.

range_ptuple, Tuple

A 3-tuple (symb, min, max) denoting the range of the parameter. Default values: min=-10 and max=10.

labelstr

Set the label associated to this series, which will be eventually shown on the legend or colorbar.

rendering_kwdict

A dictionary of keyword arguments to be passed to the renderers in order to further customize the appearance of the line. Here are some useful links for the supported plotting libraries:

colorbarbool

Toggle the visibility of the colorbar associated to the current data series. Note that a colorbar is only visible if use_cm=True and color_func is not None. Default value: True.

use_cmbool

Toggle the use of a colormap. By default, some series might use a colormap to display the necessary data. Setting this attribute to False will inform the associated renderer to use solid color. Related parameters: color_func. Default value: False.

color_func

Define a custom color mapping when use_cm=True. It can either be:

  • A numerical function supporting vectorization. The arity can be:

    • 1 argument: f(t), where t is the parameter.

    • 2 arguments: f(x, y) where x, y are the coordinates of the points.

    • 3 arguments: f(x, y, t).

  • A symbolic expression having at most as many free symbols as expr_x or expr_y.

  • None: the default value (color mapping according to the parameter).

Alias of this parameters: tp.

colorbar_ticks_formattertick_formatter_multiples_of

An object of type tick_formatter_multiples_of which will be used to place tick values on the colorbar at each multiple of a specified quantity. This only works when use_cm=True.

detect_polesbool, str

Chose whether to detect and correctly plot the roots of the denominator. There are two algorithms at work:

  1. based on the gradient of the numerical data, it introduces NaN values at locations where the steepness is greater than some threshold. This splits the line into multiple segments. To improve detection, increase the number of discretization points n and/or change the value of eps. This algorithm can be used to visualize jump discontinuities as well as essential discontinuities.

  2. a symbolic approach based on the continuous_domain function from the sympy.calculus.util module, which computes the locations of essential discontinuities. If any are found, vertical lines will be shown.

Possible options:

  • False: No poles detection

  • True: Poles detection with the numerical algorithm

  • ‘symbolic’: Poles detection with numerical and symbolic algorithms

Default value: False.

epsfloat

An arbitrary small value used by the detect_poles numerical algorithm. Before changing this value, it is recommended to increase the number of discretization points. Related parameters: detect_poles. It must be: 0 ≤ eps < ∞. Default value: 0.01.

excludelist

A list of numerical values along the parameter which are going to be excluded from the evaluation. In practice, it introduces discontinuities in the resulting line.

force_real_evalbool

By default, numerical evaluation is performed over complex numbers, which is slower but produces correct results. However, when the symbolic expression is converted to a numerical function with lambdify, the resulting function may not like to be evaluated over complex numbers. In such cases, forcing the evaluation to be performed over real numbers might be a good choice. The plotting module should be able to detect such occurences and automatically activate this option. If that is not the case, or evaluation performance is of paramount importance, set this parameter to True, but be aware that it might produce wrong results. Default value: False.

is_filledbool

Whether scatter’s markers are filled or void. Default value: True.

is_scatterbool

If True it represent a scatter plot, otherwise a continuous line. Default value: False.

line_color

For back-compatibility with old sympy.plotting. Use rendering_kw in order to fully customize the appearance of the line/scatter.

modules

Specify the evaluation modules to be used by lambdify. If not specified, the evaluation will be done with NumPy/SciPy.

n1int

Number of discretization points along the parameter to be used in the evaluation. An alias of this parameter is n. Related parameters: xscale. It must be: 2 ≤ n1 < ∞. Default value: 1000.

only_integersbool

Discretize the domain using only integer numbers. When this parameter is True, the number of discretization points is choosen by the algorithm. Default value: False.

paramsdict, optional

A dictionary mapping symbols to parameters. If provided, this dictionary enables the interactive-widgets plot.

When calling a plotting function, the parameter can be specified with:

  • a widget from the ipywidgets module.

  • a widget from the panel module.

  • a tuple of the form:

    (default, min, max, N, tick_format, label, spacing), which will instantiate a ipywidgets.widgets.widget_float.FloatSlider or a ipywidgets.widgets.widget_float.FloatLogSlider, depending on the spacing strategy. In particular:

    • default, min, maxfloat

      Default value, minimum value and maximum value of the slider, respectively. Must be finite numbers. The order of these 3 numbers is not important: the module will figure it out which is what.

    • Nint, optional

      Number of steps of the slider.

    • tick_formatstr or None, optional

      Provide a formatter for the tick value of the slider. Default to ".2f".

    • label: str, optional

      Custom text associated to the slider.

    • spacingstr, optional

      Specify the discretization spacing. Default to "linear", can be changed to "log".

Notes:

  1. parameters cannot be linked together (ie, one parameter cannot depend on another one).

  2. If a widget returns multiple numerical values (like panel.widgets.slider.RangeSlider or ipywidgets.widgets.widget_float.FloatRangeSlider), then a corresponding number of symbols must be provided.

Here follows a couple of examples. If imodule="panel":

import panel as pn
params = {
    a: (1, 0, 5), # slider from 0 to 5, with default value of 1
    b: pn.widgets.FloatSlider(value=1, start=0, end=5), # same slider as above
    (c, d): pn.widgets.RangeSlider(value=(-1, 1), start=-3, end=3, step=0.1)
}

Or with imodule="ipywidgets":

import ipywidgets as w
params = {
    a: (1, 0, 5), # slider from 0 to 5, with default value of 1
    b: w.FloatSlider(value=1, min=0, max=5), # same slider as above
    (c, d): w.FloatRangeSlider(value=(-1, 1), min=-3, max=3, step=0.1)
}

When instantiating a data series directly, params must be a dictionary mapping symbols to numerical values.

Let series be any data series. Then series.params returns a dictionary mapping symbols to numerical values.

show_in_legendbool

Toggle the visibility of the data series on the legend. Default value: True.

sum_boundint

When plotting sums, the expression will be pre-processed in order to replace lower/upper bounds set to +/- infinity with this +/- numerical value. Note: the higher this number, the slower the evaluation, but the more accurate the plot. It must be: 0 ≤ sum_bound < ∞. Default value: 1000.

txcallable

Numerical transformation function to be applied to the data on the x-axis.

tycallable

Numerical transformation function to be applied to the data on the y-axis.

xscalestr

Discretization strategy along the parameter. Possible options: [‘linear’, ‘log’] Default value: ‘linear’.

Returns:
serieslist

A list containing one instance of Parametric2DLineSeries.

See also

spb.graphics.functions_3d.line_parametric_3d, line_polar, line

Examples

>>> from sympy import symbols, cos, sin, pi, floor, log
>>> from spb import *
>>> t, u, v = symbols('t, u, v')

(Source code)

A parametric plot of a single expression (a Hypotrochoid using an equal aspect ratio), showing colorbar’s ticks at multiple of pi:

>>> graphics(
...     line_parametric_2d(
...         2 * cos(u) + 5 * cos(2 * u / 3),
...         2 * sin(u) - 5 * sin(2 * u / 3),
...         (u, 0, 6 * pi),
...         colorbar_ticks_formatter=multiples_of_pi(),
...     ),
...     aspect="equal"
... )
Plot object containing:
[0]: parametric cartesian line: (5*cos(2*u/3) + 2*cos(u), -5*sin(2*u/3) + 2*sin(u)) for u over (0, 6*pi)

(Source code, png)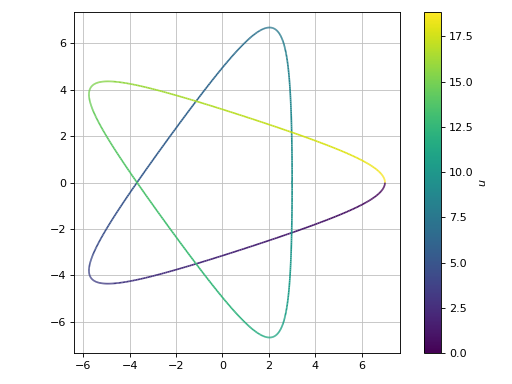

../../_images/functions_2d-12.png

A parametric plot with multiple expressions with the same range with solid line colors:

>>> graphics(
...     line_parametric_2d(2 * cos(t), sin(t), (t, 0, 2*pi), use_cm=False),
...     line_parametric_2d(cos(t), 2 * sin(t), (t, 0, 2*pi), use_cm=False),
... )
Plot object containing:
[0]: parametric cartesian line: (2*cos(t), sin(t)) for t over (0, 2*pi)
[1]: parametric cartesian line: (cos(t), 2*sin(t)) for t over (0, 2*pi)

(Source code, png)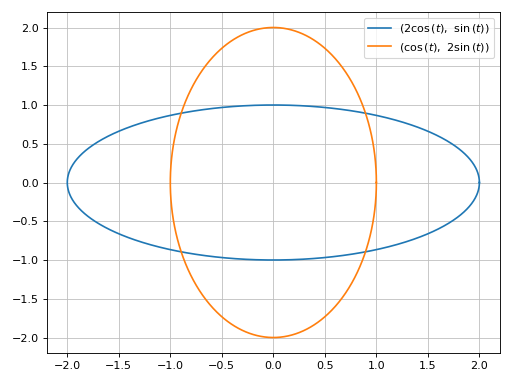

../../_images/functions_2d-13.png

A parametric plot with multiple expressions with different ranges, custom labels, custom rendering options and a transformation function applied to the discretized parameter to convert radians to degrees:

>>> import numpy as np
>>> graphics(
...     line_parametric_2d(
...         3 * cos(u), 3 * sin(u), (u, 0, 2 * pi), "u [deg]",
...         rendering_kw={"lw": 3}, tp=np.rad2deg),
...     line_parametric_2d(
...         3 * cos(2 * v), 5 * sin(4 * v), (v, 0, pi), "v [deg]",
...         tp=np.rad2deg
...     ),
...     aspect="equal"
... )
Plot object containing:
[0]: parametric cartesian line: (3*cos(u), 3*sin(u)) for u over (0, 2*pi)
[1]: parametric cartesian line: (3*cos(2*v), 5*sin(4*v)) for v over (0, pi)

(Source code, png)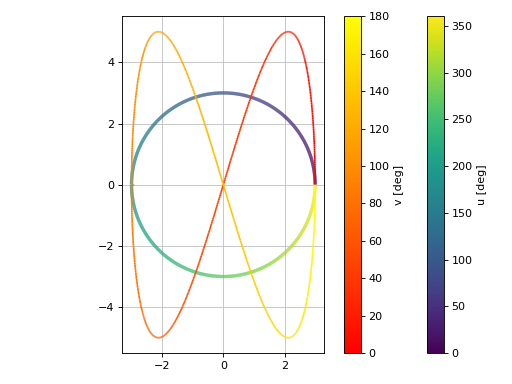

../../_images/functions_2d-14.png

Introducing discontinuities by excluding specified points:

>>> e1 = log(floor(t))*cos(t)
>>> e2 = log(floor(t))*sin(t)
>>> graphics(
...     line_parametric_2d(
...         e1, e2, (t, 1, 4*pi), exclude=list(range(1, 13))),
...     grid=False
... )
Plot object containing:
[0]: parametric cartesian line: (log(floor(t))*cos(t), log(floor(t))*sin(t)) for t over (1, 4*pi)

(Source code, png)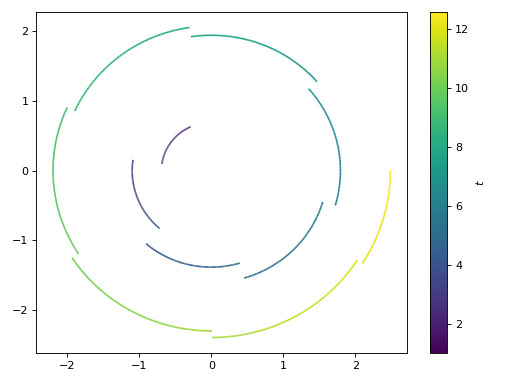

../../_images/functions_2d-15.png

Plotting a numerical function instead of a symbolic expression:

>>> import numpy as np
>>> fx = lambda t: np.sin(t) * (np.exp(np.cos(t)) - 2 * np.cos(4 * t) - np.sin(t / 12)**5)
>>> fy = lambda t: np.cos(t) * (np.exp(np.cos(t)) - 2 * np.cos(4 * t) - np.sin(t / 12)**5)
>>> graphics(
...     line_parametric_2d(fx, fy, ("t", 0, 12 * pi),
...         use_cm=False, n=2000),
...     title="Butterfly Curve",
... )

(Source code, png)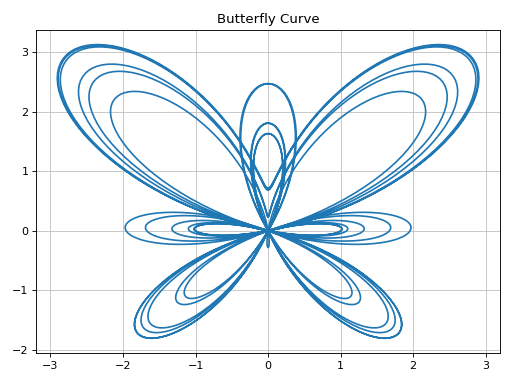

../../_images/functions_2d-16.png

Interactive-widget plot. Refer to the interactive sub-module documentation to learn more about the params dictionary. This plot illustrates:

  • the use of prange (parametric plotting range).

  • the use of the params dictionary to specify sliders in their basic form: (default, min, max).

from sympy import *
from spb import *
x, a, s, e = symbols("x a s, e")
graphics(
    line_parametric_2d(
        cos(a * x), sin(x), prange(x, s*pi, e*pi),
            params={
            a: (0.5, 0, 2),
            s: (0, 0, 2),
            e: (2, 0, 2),
        }),
    aspect="equal",
    xlim=(-1.25, 1.25), ylim=(-1.25, 1.25)
)

(Source code, small.png)

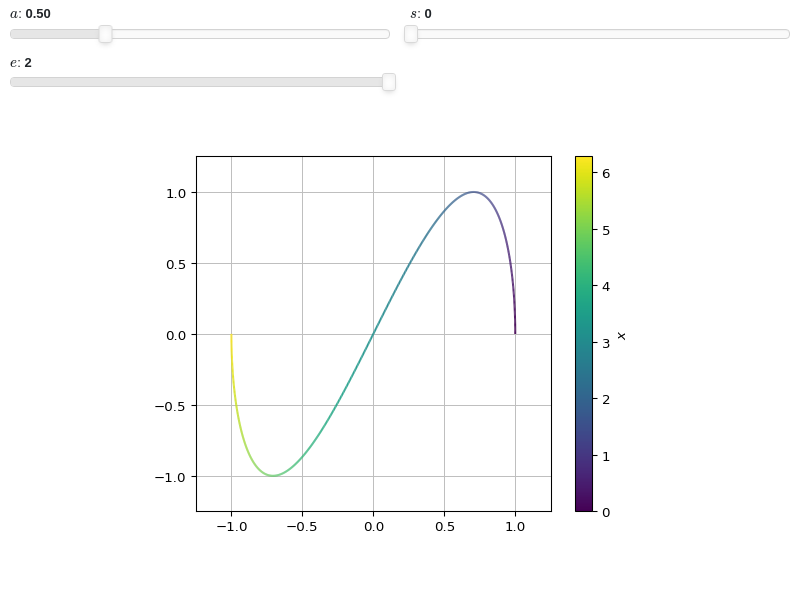
../../_images/functions_2d-17.small.png
spb.graphics.functions_2d.line_polar(expr, range_p=None, label=None, rendering_kw=None, **kwargs)[source]

Creates a 2D polar plot of a function of one variable.

Parameters:
range_ptuple, Tuple

A 3-tuple (symb, min, max) denoting the range of the parameter. Default values: min=-10 and max=10.

labelstr

Set the label associated to this series, which will be eventually shown on the legend or colorbar.

rendering_kwdict

A dictionary of keyword arguments to be passed to the renderers in order to further customize the appearance of the line. Here are some useful links for the supported plotting libraries:

color_func

Define a custom color mapping when use_cm=True. It can either be:

  • A numerical function supporting vectorization. The arity can be:

    • 1 argument: f(t), where t is the parameter.

    • 2 arguments: f(x, y) where x, y are the coordinates of the points.

    • 3 arguments: f(x, y, t).

  • A symbolic expression having at most as many free symbols as expr_x or expr_y.

  • None: the default value (color mapping according to the parameter).

Alias of this parameters: tp.

colorbarbool

Toggle the visibility of the colorbar associated to the current data series. Note that a colorbar is only visible if use_cm=True and color_func is not None. Default value: True.

colorbar_ticks_formattertick_formatter_multiples_of

An object of type tick_formatter_multiples_of which will be used to place tick values on the colorbar at each multiple of a specified quantity. This only works when use_cm=True.

detect_polesbool, str

Chose whether to detect and correctly plot the roots of the denominator. There are two algorithms at work:

  1. based on the gradient of the numerical data, it introduces NaN values at locations where the steepness is greater than some threshold. This splits the line into multiple segments. To improve detection, increase the number of discretization points n and/or change the value of eps. This algorithm can be used to visualize jump discontinuities as well as essential discontinuities.

  2. a symbolic approach based on the continuous_domain function from the sympy.calculus.util module, which computes the locations of essential discontinuities. If any are found, vertical lines will be shown.

Possible options:

  • False: No poles detection

  • True: Poles detection with the numerical algorithm

  • ‘symbolic’: Poles detection with numerical and symbolic algorithms

Default value: False.

epsfloat

An arbitrary small value used by the detect_poles numerical algorithm. Before changing this value, it is recommended to increase the number of discretization points. Related parameters: detect_poles. It must be: 0 ≤ eps < ∞. Default value: 0.01.

excludelist

A list of numerical values along the parameter which are going to be excluded from the evaluation. In practice, it introduces discontinuities in the resulting line.

expr_x

The expression representing the component along the x-axis of the parametric function. It can either be a symbolic expression representing the function of one variable to be plotted, or a numerical function of one variable, supporting vectorization. In the latter case the following keyword arguments are not supported: params, sum_bound.

expr_y

The expression representing the component along the y-axis of the parametric function. It can either be a symbolic expression representing the function of one variable to be plotted, or a numerical function of one variable, supporting vectorization. In the latter case the following keyword arguments are not supported: params, sum_bound.

force_real_evalbool

By default, numerical evaluation is performed over complex numbers, which is slower but produces correct results. However, when the symbolic expression is converted to a numerical function with lambdify, the resulting function may not like to be evaluated over complex numbers. In such cases, forcing the evaluation to be performed over real numbers might be a good choice. The plotting module should be able to detect such occurences and automatically activate this option. If that is not the case, or evaluation performance is of paramount importance, set this parameter to True, but be aware that it might produce wrong results. Default value: False.

is_filledbool

Whether scatter’s markers are filled or void. Default value: True.

is_scatterbool

If True it represent a scatter plot, otherwise a continuous line. Default value: False.

line_color

For back-compatibility with old sympy.plotting. Use rendering_kw in order to fully customize the appearance of the line/scatter.

modules

Specify the evaluation modules to be used by lambdify. If not specified, the evaluation will be done with NumPy/SciPy.

n1int

Number of discretization points along the parameter to be used in the evaluation. An alias of this parameter is n. Related parameters: xscale. It must be: 2 ≤ n1 < ∞. Default value: 1000.

only_integersbool

Discretize the domain using only integer numbers. When this parameter is True, the number of discretization points is choosen by the algorithm. Default value: False.

paramsdict, optional

A dictionary mapping symbols to parameters. If provided, this dictionary enables the interactive-widgets plot.

When calling a plotting function, the parameter can be specified with:

  • a widget from the ipywidgets module.

  • a widget from the panel module.

  • a tuple of the form:

    (default, min, max, N, tick_format, label, spacing), which will instantiate a ipywidgets.widgets.widget_float.FloatSlider or a ipywidgets.widgets.widget_float.FloatLogSlider, depending on the spacing strategy. In particular:

    • default, min, maxfloat

      Default value, minimum value and maximum value of the slider, respectively. Must be finite numbers. The order of these 3 numbers is not important: the module will figure it out which is what.

    • Nint, optional

      Number of steps of the slider.

    • tick_formatstr or None, optional

      Provide a formatter for the tick value of the slider. Default to ".2f".

    • label: str, optional

      Custom text associated to the slider.

    • spacingstr, optional

      Specify the discretization spacing. Default to "linear", can be changed to "log".

Notes:

  1. parameters cannot be linked together (ie, one parameter cannot depend on another one).

  2. If a widget returns multiple numerical values (like panel.widgets.slider.RangeSlider or ipywidgets.widgets.widget_float.FloatRangeSlider), then a corresponding number of symbols must be provided.

Here follows a couple of examples. If imodule="panel":

import panel as pn
params = {
    a: (1, 0, 5), # slider from 0 to 5, with default value of 1
    b: pn.widgets.FloatSlider(value=1, start=0, end=5), # same slider as above
    (c, d): pn.widgets.RangeSlider(value=(-1, 1), start=-3, end=3, step=0.1)
}

Or with imodule="ipywidgets":

import ipywidgets as w
params = {
    a: (1, 0, 5), # slider from 0 to 5, with default value of 1
    b: w.FloatSlider(value=1, min=0, max=5), # same slider as above
    (c, d): w.FloatRangeSlider(value=(-1, 1), min=-3, max=3, step=0.1)
}

When instantiating a data series directly, params must be a dictionary mapping symbols to numerical values.

Let series be any data series. Then series.params returns a dictionary mapping symbols to numerical values.

show_in_legendbool

Toggle the visibility of the data series on the legend. Default value: True.

sum_boundint

When plotting sums, the expression will be pre-processed in order to replace lower/upper bounds set to +/- infinity with this +/- numerical value. Note: the higher this number, the slower the evaluation, but the more accurate the plot. It must be: 0 ≤ sum_bound < ∞. Default value: 1000.

txcallable

Numerical transformation function to be applied to the data on the x-axis.

tycallable

Numerical transformation function to be applied to the data on the y-axis.

use_cmbool

Toggle the use of a colormap. By default, some series might use a colormap to display the necessary data. Setting this attribute to False will inform the associated renderer to use solid color. Related parameters: color_func. Default value: False.

xscalestr

Discretization strategy along the parameter. Possible options: [‘linear’, ‘log’] Default value: ‘linear’.

See also

line_parametric_2d, line

Examples

>>> from sympy import symbols, sin, cos, exp, pi
>>> from spb import *
>>> theta = symbols('theta')

(Source code)

Plot with cartesian axis:

>>> graphics(
...     line_polar(3 * sin(2 * theta), (theta, 0, 2*pi)),
...     aspect="equal"
... )
Plot object containing:
[0]: parametric cartesian line: (3*sin(2*theta)*cos(theta), 3*sin(theta)*sin(2*theta)) for theta over (0, 2*pi)

(Source code, png)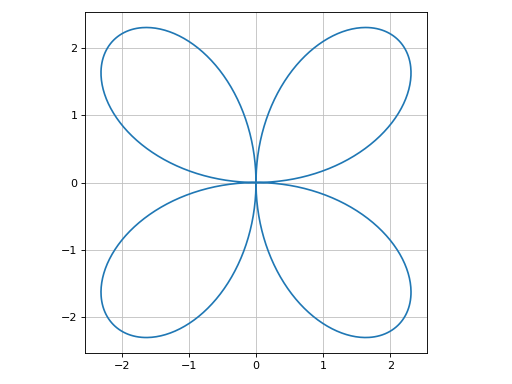

../../_images/functions_2d-19.png

Plot with polar axis:

>>> graphics(
...     line_polar(exp(sin(theta)) - 2 * cos(4 * theta), (theta, 0, 2 * pi)),
...     polar_axis=True, aspect="equal"
... )
Plot object containing:
[0]: parametric cartesian line: ((exp(sin(theta)) - 2*cos(4*theta))*cos(theta), (exp(sin(theta)) - 2*cos(4*theta))*sin(theta)) for theta over (0, 2*pi)

(Source code, png)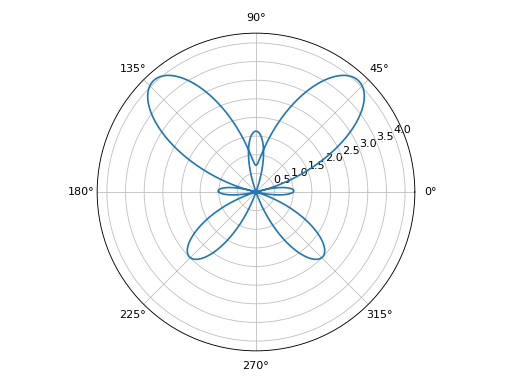

../../_images/functions_2d-20.png

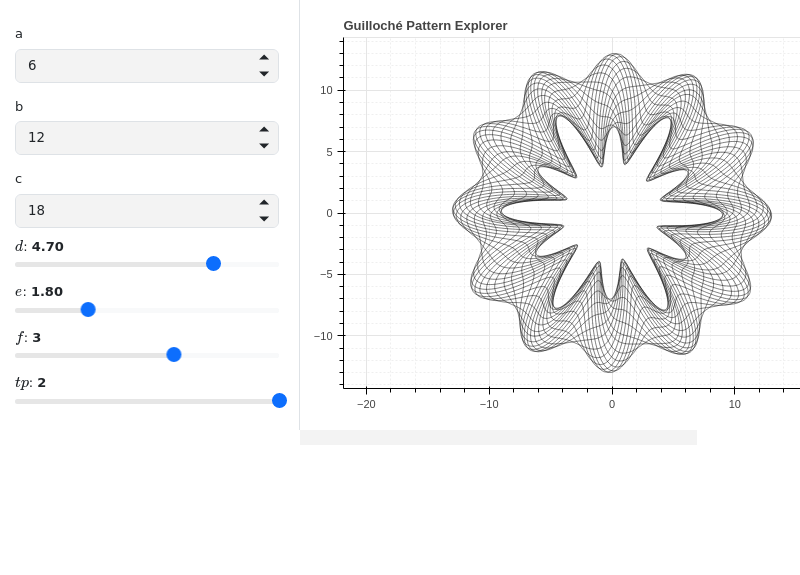
Interactive-widget plot of Guilloché Pattern. Refer to the interactive sub-module documentation to learn more about the params dictionary. This plot illustrates:

  • the use of prange (parametric plotting range).

  • the use of the params dictionary to specify the widgets to be created by Holoviz’s Panel.

from sympy import *
from spb import *
import panel as pn
a, b, c, d, e, f, theta, tp = symbols("a:f theta tp")
def func(n):
    t1 = (c + sin(a * theta + d))
    t2 = ((b + sin(b * theta + e)) - (c + sin(a * theta + d)))
    t3 = (f + sin(a * theta + n / pi))
    return t1 + t2 * t3 / 2
params = {
    a: pn.widgets.IntInput(value=6, name="a"),
    b: pn.widgets.IntInput(value=12, name="b"),
    c: pn.widgets.IntInput(value=18, name="c"),
    d: (4.7, 0, 2*pi),
    e: (1.8, 0, 2*pi),
    f: (3, 0, 5),
    tp: (2, 0, 2)
}
series = []
for n in range(20):
    series += line_polar(
        func(n), prange(theta, 0, tp*pi), params=params,
        rendering_kw={"line_color": "black", "line_width": 0.5})
graphics(
    *series,
    aspect="equal",
    layout = "sbl",
    ncols = 1,
    title="Guilloché Pattern Explorer",
    backend=BB,
    legend=False,
    servable=True,
    imodule="panel"
)

(Source code, small.png)

../../_images/functions_2d-21.small.png
spb.graphics.functions_2d.contour(expr, range_x=None, range_y=None, label=None, rendering_kw=None, colorbar=True, clabels=True, fill=True, **kwargs)[source]

Plots contour lines or filled contours of a function of two variables.

Parameters:
expr

The expression representing the function of two variables to be plotted. It can be a:

  • Symbolic expression.

  • Numerical function of two variable, supporting vectorization. In this case the following keyword arguments are not supported: params.

range_xtuple, Tuple

A 3-tuple (symb, min, max) denoting the range of the x variable. Default values: min=-10 and max=10.

range_ytuple, Tuple

A 3-tuple (symb, min, max) denoting the range of the y variable. Default values: min=-10 and max=10.

labelstr

Set the label associated to this series, which will be eventually shown on the legend or colorbar.

rendering_kwdict

A dictionary of keyword arguments to be passed to the renderers in order to further customize the appearance of the contour. Here are some useful links for the supported plotting libraries:

colorbarbool

Toggle the visibility of the colorbar associated to the current data series. Note that a colorbar is only visible if use_cm=True and color_func is not None. Default value: True.

color_func

Define a custom color mapping. It can either be:

  • A numerical function supporting vectorization. The arity can be:

    • 2 arguments: f(x, y) where x, y are the coordinates of the points.

    • 3 arguments: f(x, y, z) where x, y, z are the coordinates of the points.

  • A symbolic expression having at most as many free symbols as expr.

  • None: the default value (color mapping according to the z coordinate).

colorbar_ticks_formattertick_formatter_multiples_of

An object of type tick_formatter_multiples_of which will be used to place tick values on the colorbar at each multiple of a specified quantity. This only works when use_cm=True.

force_real_evalbool

By default, numerical evaluation is performed over complex numbers, which is slower but produces correct results. However, when the symbolic expression is converted to a numerical function with lambdify, the resulting function may not like to be evaluated over complex numbers. In such cases, forcing the evaluation to be performed over real numbers might be a good choice. The plotting module should be able to detect such occurences and automatically activate this option. If that is not the case, or evaluation performance is of paramount importance, set this parameter to True, but be aware that it might produce wrong results. Default value: False.

is_filledbool

If True, use filled contours. Otherwise, use line contours. Relatated parameters: show_clabels. Default value: True.

is_polarbool

If True, requests a polar discretization. In this case, range_x represents the radius, while range_y represents the angle. Default value: False.

modules

Specify the evaluation modules to be used by lambdify. If not specified, the evaluation will be done with NumPy/SciPy.

n1int

Number of discretization points along the x-axis to be used in the evaluation. Related parameters: xscale. It must be: 2 ≤ n1 < ∞. Default value: 100.

n2int

Number of discretization points along the y-axis to be used in the evaluation. Related parameters: yscale. It must be: 2 ≤ n2 < ∞. Default value: 100.

only_integersbool

Discretize the domain using only integer numbers. When this parameter is True, the number of discretization points is choosen by the algorithm. Default value: False.

paramsdict, optional

A dictionary mapping symbols to parameters. If provided, this dictionary enables the interactive-widgets plot.

When calling a plotting function, the parameter can be specified with:

  • a widget from the ipywidgets module.

  • a widget from the panel module.

  • a tuple of the form:

    (default, min, max, N, tick_format, label, spacing), which will instantiate a ipywidgets.widgets.widget_float.FloatSlider or a ipywidgets.widgets.widget_float.FloatLogSlider, depending on the spacing strategy. In particular:

    • default, min, maxfloat

      Default value, minimum value and maximum value of the slider, respectively. Must be finite numbers. The order of these 3 numbers is not important: the module will figure it out which is what.

    • Nint, optional

      Number of steps of the slider.

    • tick_formatstr or None, optional

      Provide a formatter for the tick value of the slider. Default to ".2f".

    • label: str, optional

      Custom text associated to the slider.

    • spacingstr, optional

      Specify the discretization spacing. Default to "linear", can be changed to "log".

Notes:

  1. parameters cannot be linked together (ie, one parameter cannot depend on another one).

  2. If a widget returns multiple numerical values (like panel.widgets.slider.RangeSlider or ipywidgets.widgets.widget_float.FloatRangeSlider), then a corresponding number of symbols must be provided.

Here follows a couple of examples. If imodule="panel":

import panel as pn
params = {
    a: (1, 0, 5), # slider from 0 to 5, with default value of 1
    b: pn.widgets.FloatSlider(value=1, start=0, end=5), # same slider as above
    (c, d): pn.widgets.RangeSlider(value=(-1, 1), start=-3, end=3, step=0.1)
}

Or with imodule="ipywidgets":

import ipywidgets as w
params = {
    a: (1, 0, 5), # slider from 0 to 5, with default value of 1
    b: w.FloatSlider(value=1, min=0, max=5), # same slider as above
    (c, d): w.FloatRangeSlider(value=(-1, 1), min=-3, max=3, step=0.1)
}

When instantiating a data series directly, params must be a dictionary mapping symbols to numerical values.

Let series be any data series. Then series.params returns a dictionary mapping symbols to numerical values.

show_clabelsbool

Toggle the label’s visibility of contour lines. It only works when is_filled=False. Note that some backend might not implement this feature. Relatated parameters: is_filled. Default value: True.

show_in_legendbool

Toggle the visibility of the data series on the legend. Default value: True.

sum_boundint

When plotting sums, the expression will be pre-processed in order to replace lower/upper bounds set to +/- infinity with this +/- numerical value. Note: the higher this number, the slower the evaluation, but the more accurate the plot. It must be: 0 ≤ sum_bound < ∞. Default value: 1000.

surface_color

For back-compatibility with old sympy.plotting. Use rendering_kw in order to fully customize the appearance of the surface.

txcallable

Numerical transformation function to be applied to the data on the x-axis.

tycallable

Numerical transformation function to be applied to the data on the y-axis.

tzcallable

Numerical transformation function to be applied to the data on the z-axis.

use_cmbool

Toggle the use of a colormap. By default, some series might use a colormap to display the necessary data. Setting this attribute to False will inform the associated renderer to use solid color. Related parameters: color_func. Default value: False.

xscalestr

Discretization strategy along the x-direction. Related parameters: n1. Possible options: [‘linear’, ‘log’] Default value: ‘linear’.

yscalestr

Discretization strategy along the y-direction. Related parameters: n2. Possible options: [‘linear’, ‘log’] Default value: ‘linear’.

Returns:
serieslist

A list containing one instance of ContourSeries.

See also

spb.graphics.functions_3d.surface

Examples

>>> from sympy import symbols, cos, exp, sin, pi, Eq, Add
>>> from spb import *
>>> x, y = symbols('x, y')

(Source code)

Filled contours of a function of two variables.

>>> graphics(
...     contour(
...         cos((x**2 + y**2)) * exp(-(x**2 + y**2) / 10),
...         (x, -5, 5), (y, -5, 5)
...     ),
...     grid=False
... )
Plot object containing:
[0]: contour: exp(-x**2/10 - y**2/10)*cos(x**2 + y**2) for x over (-5, 5) and y over (-5, 5)

(Source code, png)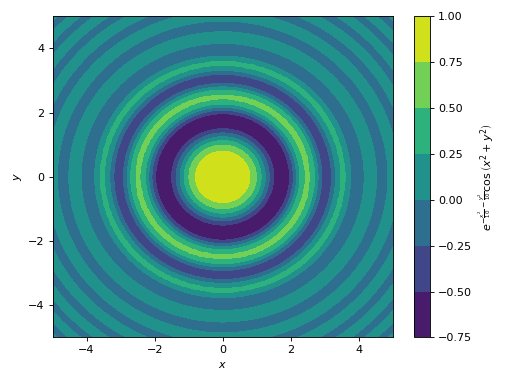

../../_images/functions_2d-23.png

Line contours of a function of two variables, with ticks formatted as multiples of pi/n.

>>> expr = 5 * (cos(x) - 0.2 * sin(y))**2 + 5 * (-0.2 * cos(x) + sin(y))**2
>>> graphics(
...     contour(expr, (x, 0, 2 * pi), (y, 0, 2 * pi), fill=False),
...     x_ticks_formatter=multiples_of_pi_over_2(),
...     y_ticks_formatter=multiples_of_pi_over_3(),
...     aspect="equal"
... )
Plot object containing:
[0]: contour: 5*(-0.2*sin(y) + cos(x))**2 + 5*(sin(y) - 0.2*cos(x))**2 for x over (0, 2*pi) and y over (0, 2*pi)

(Source code, png)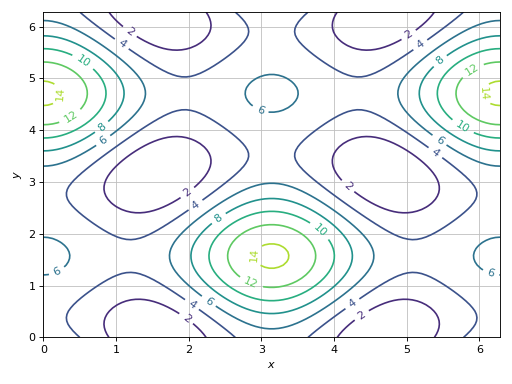

../../_images/functions_2d-24.png

Combining together filled and line contours. Use a custom label on the colorbar of the filled contour.

>>> expr = 5 * (cos(x) - 0.2 * sin(y))**2 + 5 * (-0.2 * cos(x) + sin(y))**2
>>> graphics(
...     contour(expr, (x, 0, 2 * pi), (y, 0, 2 * pi), "z",
...         rendering_kw={"cmap": "coolwarm"}),
...     contour(expr, (x, 0, 2 * pi), (y, 0, 2 * pi),
...         rendering_kw={"colors": "k", "cmap": None, "linewidths": 0.75},
...         fill=False),
...     x_ticks_formatter=multiples_of_pi_over_2(),
...     y_ticks_formatter=multiples_of_pi_over_3(),
...     aspect="equal", grid=False
... )
Plot object containing:
[0]: contour: 5*(-0.2*sin(y) + cos(x))**2 + 5*(sin(y) - 0.2*cos(x))**2 for x over (0, 2*pi) and y over (0, 2*pi)
[1]: contour: 5*(-0.2*sin(y) + cos(x))**2 + 5*(sin(y) - 0.2*cos(x))**2 for x over (0, 2*pi) and y over (0, 2*pi)

(Source code, png)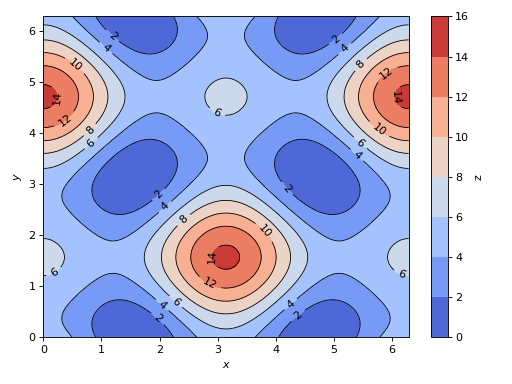

../../_images/functions_2d-25.png

Visually inspect the solutions of a system of 2 non-linear equations. The intersections between the contour lines represent the solutions.

>>> eq1 = Eq((cos(x) - sin(y) / 2)**2 + 3 * (-sin(x) + cos(y) / 2)**2, 2)
>>> eq2 = Eq((cos(x) - 2 * sin(y))**2 - (sin(x) + 2 * cos(y))**2, 3)
>>> graphics(
...     contour(
...         eq1.lhs - eq1.rhs, (x, 0, 2 * pi), (y, 0, 2 * pi),
...         rendering_kw={"levels": [0]},
...         fill=False, clabels=False),
...     contour(
...         eq2.lhs - eq2.rhs, (x, 0, 2 * pi), (y, 0, 2 * pi),
...         rendering_kw={"levels": [0]},
...         fill=False, clabels=False),
... )
Plot object containing:
[0]: contour: 3*(-sin(x) + cos(y)/2)**2 + (-sin(y)/2 + cos(x))**2 - 2 for x over (0, 2*pi) and y over (0, 2*pi)
[1]: contour: -(sin(x) + 2*cos(y))**2 + (-2*sin(y) + cos(x))**2 - 3 for x over (0, 2*pi) and y over (0, 2*pi)

(Source code, png)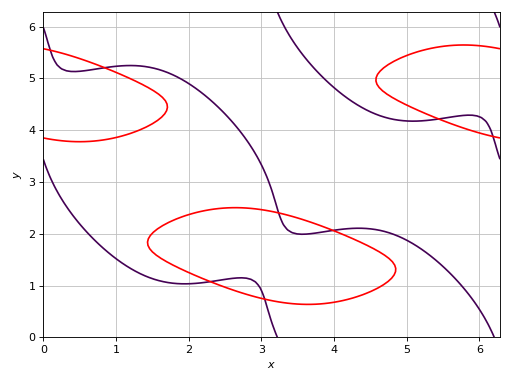

../../_images/functions_2d-26.png

Contour plot with polar axis:

>>> r, theta = symbols("r, theta")
>>> graphics(
...     contour(
...         sin(2 * r) * cos(theta), (theta, 0, 2*pi), (r, 0, 7),
...         rendering_kw={"levels": 100}
...     ),
...     polar_axis=True, aspect="equal"
... )
Plot object containing:
[0]: contour: sin(2*r)*cos(theta) for theta over (0, 2*pi) and r over (0, 7)

(Source code, png)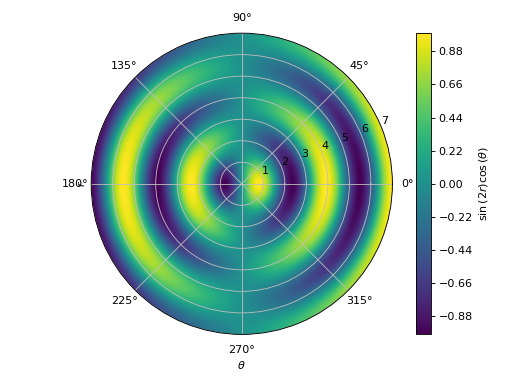

../../_images/functions_2d-27.png

Interactive-widget plot. Refer to the interactive sub-module documentation to learn more about the params dictionary. This plot illustrates:

  • the use of prange (parametric plotting range).

  • the use of the params dictionary to specify sliders in their basic form: (default, min, max).

  • the use of panel.widgets.slider.RangeSlider, which is a 2-values widget.

from sympy import *
from spb import *
import panel as pn
x, y, a, b = symbols("x y a b")
x_min, x_max, y_min, y_max = symbols("x_min x_max y_min y_max")
expr = (cos(x) + a * sin(x) * sin(y) - b * sin(x) * cos(y))**2
graphics(
    contour(
        expr, prange(x, x_min*pi, x_max*pi), prange(y, y_min*pi, y_max*pi),
        params={
            a: (1, 0, 2), b: (1, 0, 2),
            (x_min, x_max): pn.widgets.RangeSlider(
                value=(-1, 1), start=-3, end=3, step=0.1),
            (y_min, y_max): pn.widgets.RangeSlider(
                value=(-1, 1), start=-3, end=3, step=0.1),
        }),
    grid=False
)

(Source code, small.png)

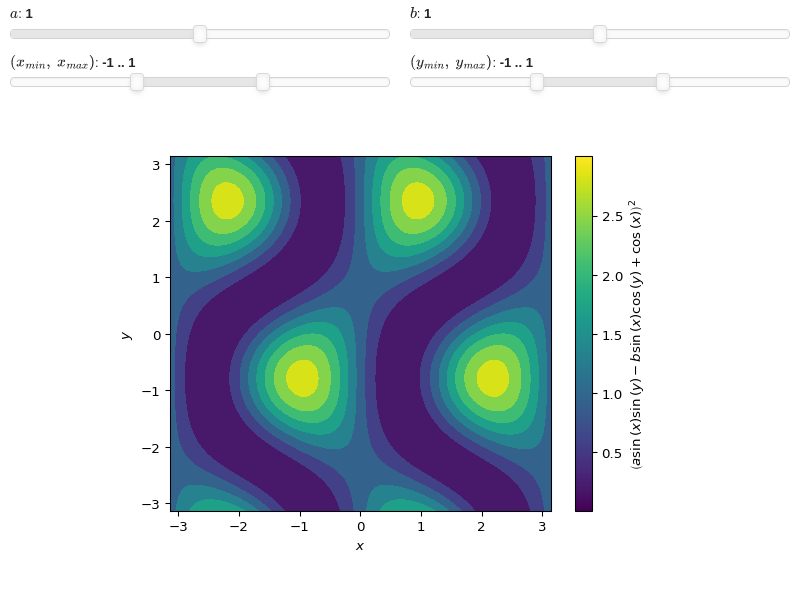
../../_images/functions_2d-28.small.png
spb.graphics.functions_2d.implicit_2d(f, range_x=None, range_y=None, label=None, rendering_kw=None, color=None, border_color=None, border_kw=None, **kwargs)[source]

Plot implicit equations / inequalities.

implicit_2d, by default, generates a contour using a mesh grid of fixednumber of points. The greater the number of points, the better the results, but also the greater the memory used. By setting adaptive=True, interval arithmetic will be used to plot functions. If the expression cannot be plotted using interval arithmetic, it defaults to generating a contour using a mesh grid. With interval arithmetic, the line width can become very small; in those cases, it is better to use the mesh grid approach.

Parameters:
fRelational, Boolean, Expr

The equation / inequality that is to be plotted.

range_xtuple, Tuple

A 3-tuple (symb, min, max) denoting the range of the x variable. Default values: min=-10 and max=10.

range_ytuple, Tuple

A 3-tuple (symb, min, max) denoting the range of the y variable. Default values: min=-10 and max=10.

labelstr

Set the label associated to this series, which will be eventually shown on the legend or colorbar.

rendering_kwdict

A dictionary of keyword arguments to be passed to the renderers in order to further customize the appearance of the contour. Here are some useful links for the supported plotting libraries:

colorstr, optional

Specify the color of lines/regions. Default to None (automatic coloring by the backend).

border_colorstr or bool, optional

If given, a limiting border will be added when plotting inequalities (<, <=, >, >=). Use border_kw if more customization options are required.

border_kwdict, optional

If given, a limiting border will be added when plotting inequalities (<, <=, >, >=). This is a dictionary of keywords/values which is passed to the backend’s function to customize the appearance of the limiting border. Refer to the plotting library (backend) manual for more informations.

adaptivebool

Select the evaluation strategy to be used. If False, the internal algorithm uses a mesh grid approach. In such case, Boolean combinations of expressions cannot be plotted. If True, the internal algorithm uses interval arithmetic. If the expression cannot be plotted with interval arithmetic, it switches to the meshgrid approach. Default value: False.

colorbarbool

Toggle the visibility of the colorbar associated to the current data series. Note that a colorbar is only visible if use_cm=True and color_func is not None. Default value: True.

depthint

The depth of recursion for adaptive grid. Think of the resulting plot as a picture composed by pixels. Increasing depth will increase the number of pixels, thus obtaining a more accurate plot, at the cost of evaluation speed and possibly readability (if the figure has small size). It must be: 0 ≤ depth ≤ 4. Default value: 0.

force_real_evalbool

By default, numerical evaluation is performed over complex numbers, which is slower but produces correct results. However, when the symbolic expression is converted to a numerical function with lambdify, the resulting function may not like to be evaluated over complex numbers. In such cases, forcing the evaluation to be performed over real numbers might be a good choice. The plotting module should be able to detect such occurences and automatically activate this option. If that is not the case, or evaluation performance is of paramount importance, set this parameter to True, but be aware that it might produce wrong results. Default value: False.

modules

Specify the evaluation modules to be used by lambdify. If not specified, the evaluation will be done with NumPy/SciPy.

n1int

Number of discretization points along the x-axis to be used in the evaluation, when adaptive=False. Related parameters: adaptive, xscale. It must be: 2 ≤ n1 < ∞. Default value: 100.

n2int

Number of discretization points along the y-axis to be used in the evaluation, when adaptive=False. Related parameters: adaptive, yscale. It must be: 2 ≤ n2 < ∞. Default value: 100.

only_integersbool

Discretize the domain using only integer numbers. When this parameter is True, the number of discretization points is choosen by the algorithm. Default value: False.

paramsdict, optional

A dictionary mapping symbols to parameters. If provided, this dictionary enables the interactive-widgets plot.

When calling a plotting function, the parameter can be specified with:

  • a widget from the ipywidgets module.

  • a widget from the panel module.

  • a tuple of the form:

    (default, min, max, N, tick_format, label, spacing), which will instantiate a ipywidgets.widgets.widget_float.FloatSlider or a ipywidgets.widgets.widget_float.FloatLogSlider, depending on the spacing strategy. In particular:

    • default, min, maxfloat

      Default value, minimum value and maximum value of the slider, respectively. Must be finite numbers. The order of these 3 numbers is not important: the module will figure it out which is what.

    • Nint, optional

      Number of steps of the slider.

    • tick_formatstr or None, optional

      Provide a formatter for the tick value of the slider. Default to ".2f".

    • label: str, optional

      Custom text associated to the slider.

    • spacingstr, optional

      Specify the discretization spacing. Default to "linear", can be changed to "log".

Notes:

  1. parameters cannot be linked together (ie, one parameter cannot depend on another one).

  2. If a widget returns multiple numerical values (like panel.widgets.slider.RangeSlider or ipywidgets.widgets.widget_float.FloatRangeSlider), then a corresponding number of symbols must be provided.

Here follows a couple of examples. If imodule="panel":

import panel as pn
params = {
    a: (1, 0, 5), # slider from 0 to 5, with default value of 1
    b: pn.widgets.FloatSlider(value=1, start=0, end=5), # same slider as above
    (c, d): pn.widgets.RangeSlider(value=(-1, 1), start=-3, end=3, step=0.1)
}

Or with imodule="ipywidgets":

import ipywidgets as w
params = {
    a: (1, 0, 5), # slider from 0 to 5, with default value of 1
    b: w.FloatSlider(value=1, min=0, max=5), # same slider as above
    (c, d): w.FloatRangeSlider(value=(-1, 1), min=-3, max=3, step=0.1)
}

When instantiating a data series directly, params must be a dictionary mapping symbols to numerical values.

Let series be any data series. Then series.params returns a dictionary mapping symbols to numerical values.

show_in_legendbool

Toggle the visibility of the data series on the legend. Default value: True.

sum_boundint

When plotting sums, the expression will be pre-processed in order to replace lower/upper bounds set to +/- infinity with this +/- numerical value. Note: the higher this number, the slower the evaluation, but the more accurate the plot. It must be: 0 ≤ sum_bound < ∞. Default value: 1000.

use_cmbool

Toggle the use of a colormap. By default, some series might use a colormap to display the necessary data. Setting this attribute to False will inform the associated renderer to use solid color. Related parameters: color_func. Default value: False.

xscalestr

Discretization strategy along the x-direction. Related parameters: n1. Possible options: [‘linear’, ‘log’] Default value: ‘linear’.

yscalestr

Discretization strategy along the y-direction. Related parameters: n2. Possible options: [‘linear’, ‘log’] Default value: ‘linear’.

Returns:
serieslist

A list containing at most two instances of Implicit2DSeries.

See also

line, spb.graphics.functions_3d.implicit_3d

Examples

Plot expressions:

>>> from sympy import symbols, Ne, Eq, And, sin, cos, pi, log, latex
>>> from spb import *
>>> x, y = symbols('x y')

(Source code)

Plot a line representing an equality:

>>> graphics(implicit_2d(x - 1, (x, -5, 5), (y, -5, 5)))
Plot object containing:
[0]: Implicit expression: Eq(x - 1, 0) for x over (-5, 5) and y over (-5, 5)

(Source code, png)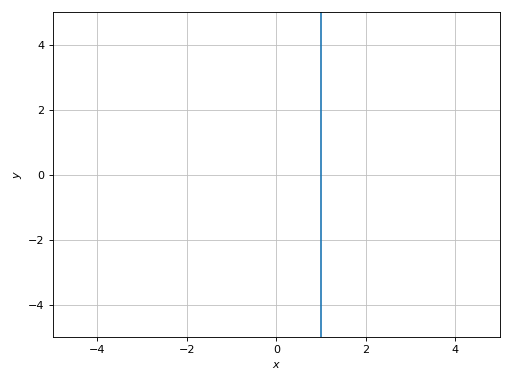

../../_images/functions_2d-30.png

Plot a region:

>>> graphics(
...     implicit_2d(y > x**2, (x, -5, 5), (y, -10, 10), n=150),
...     grid=False)
Plot object containing:
[0]: Implicit expression: y > x**2 for x over (-5, 5) and y over (-10, 10)

(Source code, png)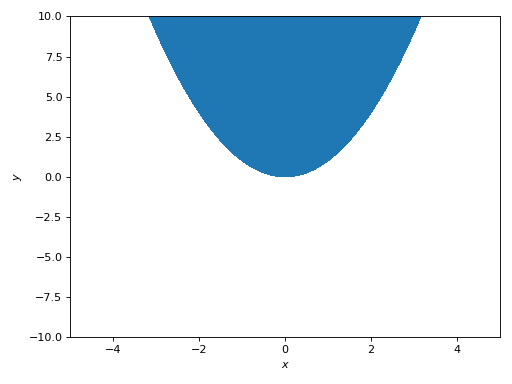

../../_images/functions_2d-31.png

Plot a region using a custom color, highlights the limiting border and customize its appearance.

>>> expr = 4 * (cos(x) - sin(y) / 5)**2 + 4 * (-cos(x) / 5 + sin(y))**2
>>> graphics(
...     implicit_2d(
...         expr <= pi, (x, -pi, pi), (y, -pi, pi),
...         color="gold", border_color="k",
...         border_kw={"linestyles": "-.", "linewidths": 1}
...     ),
...     grid=False
... )
Plot object containing:
[0]: Implicit expression: 4*(-sin(y)/5 + cos(x))**2 + 4*(sin(y) - cos(x)/5)**2 <= pi for x over (-pi, pi) and y over (-pi, pi)
[1]: Implicit expression: Eq(-4*(-sin(y)/5 + cos(x))**2 - 4*(sin(y) - cos(x)/5)**2 + pi, 0) for x over (-pi, pi) and y over (-pi, pi)

(Source code, png)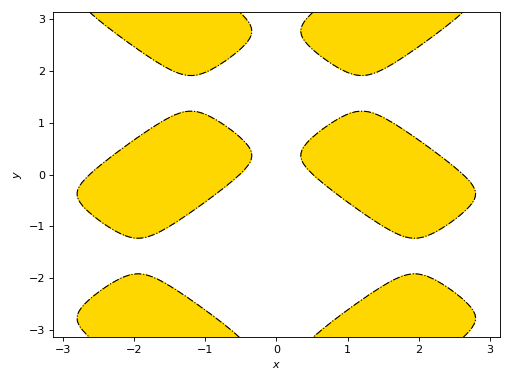

../../_images/functions_2d-32.png

Boolean expressions will be plotted with the adaptive algorithm. Note the thin width of lines:

>>> graphics(
...     implicit_2d(
...         Eq(y, sin(x)) & (y > 0), (x, -2 * pi, 2 * pi), (y, -4, 4)),
...     implicit_2d(
...         Eq(y, sin(x)) & (y < 0), (x, -2 * pi, 2 * pi), (y, -4, 4)),
...     ylim=(-2, 2)
... )
Plot object containing:
[0]: Implicit expression: (y > 0) & Eq(y, sin(x)) for x over (-2*pi, 2*pi) and y over (-4, 4)
[1]: Implicit expression: (y < 0) & Eq(y, sin(x)) for x over (-2*pi, 2*pi) and y over (-4, 4)

(Source code, png)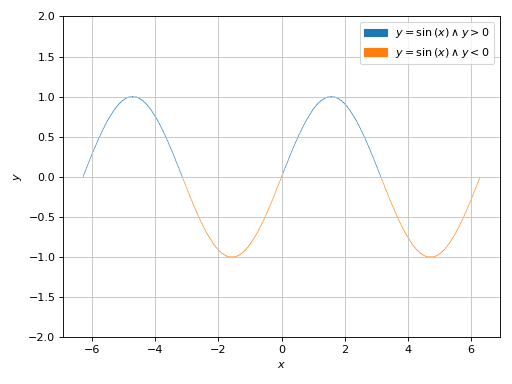

../../_images/functions_2d-33.png

Plotting multiple implicit expressions and setting labels:

>>> V, t, b, L = symbols("V, t, b, L")
>>> L_array = [5, 10, 15, 20, 25]
>>> b_val = 0.0032
>>> expr = b * V * 0.277 * t - b * L - log(1 + b * V * 0.277 * t)
>>> series = []
>>> for L_val in L_array:
...     series += implicit_2d(
...         expr.subs({b: b_val, L: L_val}), (t, 0, 3), (V, 0, 1000),
...         label="L = %s" % L_val)
>>> graphics(*series)
Plot object containing:
[0]: Implicit expression: Eq(0.0008864*V*t - log(0.0008864*V*t + 1) - 0.016, 0) for t over (0, 3) and V over (0, 1000)
[1]: Implicit expression: Eq(0.0008864*V*t - log(0.0008864*V*t + 1) - 0.032, 0) for t over (0, 3) and V over (0, 1000)
[2]: Implicit expression: Eq(0.0008864*V*t - log(0.0008864*V*t + 1) - 0.048, 0) for t over (0, 3) and V over (0, 1000)
[3]: Implicit expression: Eq(0.0008864*V*t - log(0.0008864*V*t + 1) - 0.064, 0) for t over (0, 3) and V over (0, 1000)
[4]: Implicit expression: Eq(0.0008864*V*t - log(0.0008864*V*t + 1) - 0.08, 0) for t over (0, 3) and V over (0, 1000)

(Source code, png)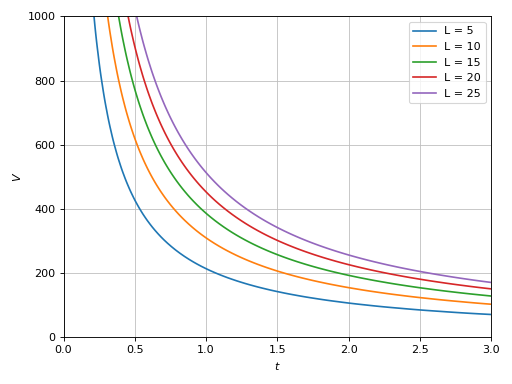

../../_images/functions_2d-34.png

Comparison of similar expressions plotted with different algorithms. Note:

  1. Adaptive algorithm (adaptive=True) can be used with any expression, but it usually creates lines with variable thickness. The depth keyword argument can be used to improve the accuracy, but reduces line thickness even further.

  2. Mesh grid algorithm (adaptive=False) creates lines with constant thickness.

>>> expr1 = Eq(x * y - 20, 15 * y)
>>> expr2 = Eq((x - 3) * y - 20, 15 * y)
>>> expr3 = Eq((x - 6) * y - 20, 15 * y)
>>> ranges = (x, 15, 30), (y, 0, 50)
>>> graphics(
...    implicit_2d(
...        expr1, *ranges, adaptive=True, depth=0,
...        label="adaptive=True, depth=0"),
...    implicit_2d(
...        expr2, *ranges, adaptive=True, depth=1,
...        label="adaptive=True, depth=1"),
...    implicit_2d(
...        expr3, *ranges, adaptive=False, label="adaptive=False"),
...    grid=False
... )
Plot object containing:
[0]: Implicit expression: Eq(x*y - 20, 15*y) for x over (15, 30) and y over (0, 50)
[1]: Implicit expression: Eq(y*(x - 3) - 20, 15*y) for x over (15, 30) and y over (0, 50)
[2]: Implicit expression: Eq(y*(x - 6) - 20, 15*y) for x over (15, 30) and y over (0, 50)

(Source code, png)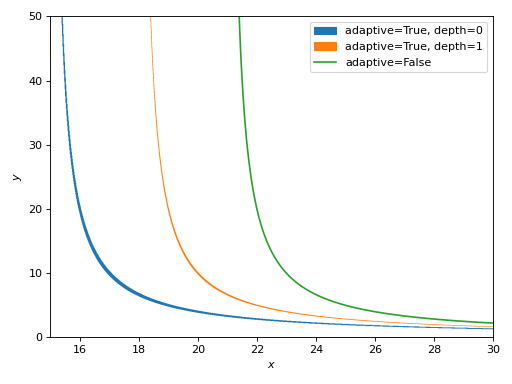

../../_images/functions_2d-35.png

If the expression is plotted with the adaptive algorithm and it produces “low-quality” results, maybe it’s possible to rewrite it in order to use the mesh grid approach (contours). For example:

>>> from spb import plotgrid
>>> expr = Ne(x*y, 1)
>>> p1 = graphics(
...     implicit_2d(expr, (x, -10, 10), (y, -10, 10)),
...     grid=False, title="$%s$ : First approach" % latex(expr),
...     aspect="equal", show=False)
>>> p2 = graphics(
...     implicit_2d(x < 20, (x, -10, 10), (y, -10, 10)),
...     implicit_2d(Eq(*expr.args), (x, -10, 10), (y, -10, 10),
...         color="w", show_in_legend=False),
...     grid=False, title="$%s$ : Second approach" % latex(expr),
...     aspect="equal", show=False)
>>> plotgrid(p1, p2, nc=2)

(Source code, png)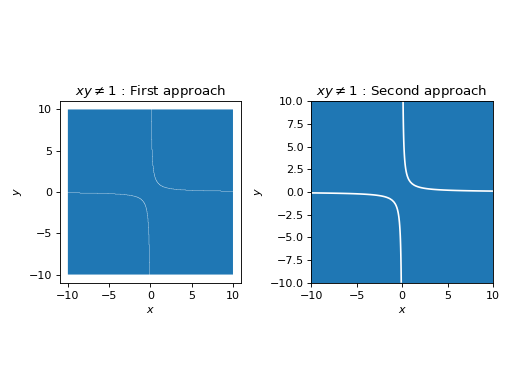

../../_images/functions_2d-36.png

Interactive-widget implicit plot. Refer to the interactive sub-module documentation to learn more about the params dictionary. This plot illustrates:

  • the use of prange (parametric plotting range).

  • the use of the params dictionary to specify sliders in their basic form: (default, min, max).

  • the use of panel.widgets.slider.RangeSlider, which is a 2-values widget.

from sympy import *
from spb import *
import panel as pn
x, y, a, b, c, d = symbols("x, y, a, b, c, d")
y_min, y_max = symbols("y_min, y_max")
expr = Eq(a * x**2 - b * x + c, d * y + y**2)
graphics(
    implicit_2d(expr, (x, -2, 2), prange(y, y_min, y_max),
        params={
            a: (10, -15, 15),
            b: (7, -15, 15),
            c: (3, -15, 15),
            d: (2, -15, 15),
            (y_min, y_max): pn.widgets.RangeSlider(
                value=(-10, 10), start=-15, end=15, step=0.1)
        }, n=150),
    ylim=(-10, 10))

(Source code, small.png)

../../_images/functions_2d-37.small.png
spb.graphics.functions_2d.list_2d(list_x, list_y, label=None, rendering_kw=None, **kwargs)[source]

Plots lists of coordinates.

Parameters:
list_x

Coordinates for the x-axis. It can be a list or a numper array.

list_y

Coordinates for the y-axis. It can be a list or a numper array.

labelstr

Set the label associated to this series, which will be eventually shown on the legend or colorbar.

rendering_kwdict

A dictionary of keyword arguments to be passed to the renderers in order to further customize the appearance of the line. Here are some useful links for the supported plotting libraries:

color_funccallable

A color function to be applied to the numerical data. It can be:

  • None: no color function.

  • callable: a function accepting:

    • no arguments: this can be used to return an array of precomputed values.

    • two arguments, the x, y coordinates.

colorbarbool

Toggle the visibility of the colorbar associated to the current data series. Note that a colorbar is only visible if use_cm=True and color_func is not None. Default value: True.

colorbar_ticks_formattertick_formatter_multiples_of

An object of type tick_formatter_multiples_of which will be used to place tick values on the colorbar at each multiple of a specified quantity. This only works when use_cm=True.

is_filledbool

Whether scatter’s markers are filled or void. Default value: True.

is_scatterbool

If True it represent a scatter plot, otherwise a continuous line. Default value: False.

line_color

For back-compatibility with old sympy.plotting. Use rendering_kw in order to fully customize the appearance of the line/scatter.

paramsdict, optional

A dictionary mapping symbols to parameters. If provided, this dictionary enables the interactive-widgets plot.

When calling a plotting function, the parameter can be specified with:

  • a widget from the ipywidgets module.

  • a widget from the panel module.

  • a tuple of the form:

    (default, min, max, N, tick_format, label, spacing), which will instantiate a ipywidgets.widgets.widget_float.FloatSlider or a ipywidgets.widgets.widget_float.FloatLogSlider, depending on the spacing strategy. In particular:

    • default, min, maxfloat

      Default value, minimum value and maximum value of the slider, respectively. Must be finite numbers. The order of these 3 numbers is not important: the module will figure it out which is what.

    • Nint, optional

      Number of steps of the slider.

    • tick_formatstr or None, optional

      Provide a formatter for the tick value of the slider. Default to ".2f".

    • label: str, optional

      Custom text associated to the slider.

    • spacingstr, optional

      Specify the discretization spacing. Default to "linear", can be changed to "log".

Notes:

  1. parameters cannot be linked together (ie, one parameter cannot depend on another one).

  2. If a widget returns multiple numerical values (like panel.widgets.slider.RangeSlider or ipywidgets.widgets.widget_float.FloatRangeSlider), then a corresponding number of symbols must be provided.

Here follows a couple of examples. If imodule="panel":

import panel as pn
params = {
    a: (1, 0, 5), # slider from 0 to 5, with default value of 1
    b: pn.widgets.FloatSlider(value=1, start=0, end=5), # same slider as above
    (c, d): pn.widgets.RangeSlider(value=(-1, 1), start=-3, end=3, step=0.1)
}

Or with imodule="ipywidgets":

import ipywidgets as w
params = {
    a: (1, 0, 5), # slider from 0 to 5, with default value of 1
    b: w.FloatSlider(value=1, min=0, max=5), # same slider as above
    (c, d): w.FloatRangeSlider(value=(-1, 1), min=-3, max=3, step=0.1)
}

When instantiating a data series directly, params must be a dictionary mapping symbols to numerical values.

Let series be any data series. Then series.params returns a dictionary mapping symbols to numerical values.

show_in_legendbool

Toggle the visibility of the data series on the legend. Default value: True.

stepsNoneType, bool, str

If set, it connects consecutive points with steps rather than straight segments. Possible options: [‘pre’, ‘post’, ‘mid’, True, False, None] Default value: False.

txcallable

Numerical transformation function to be applied to the data on the x-axis.

tycallable

Numerical transformation function to be applied to the data on the y-axis.

unwrapbool, dict

Whether to use numpy.unwrap() on the computed coordinates in order to get rid of discontinuities. It can be:

  • False: do not use np.unwrap().

  • True: use np.unwrap() with default keyword arguments.

  • dictionary of keyword arguments passed to np.unwrap().

use_cmbool

Toggle the use of a colormap. By default, some series might use a colormap to display the necessary data. Setting this attribute to False will inform the associated renderer to use solid color. Related parameters: color_func. Default value: False.

Returns:
serieslist

A list containing one instance of List2DSeries.

See also

line, spb.graphics.functions_3d.list_3d

Examples

>>> from sympy import symbols, sin, cos
>>> from spb import *
>>> x = symbols('x')

(Source code)

Plot the coordinates of a single function:

>>> xx = [t / 100 * 6 - 3 for t in list(range(101))]
>>> yy = [cos(x).evalf(subs={x: t}) for t in xx]
>>> graphics(list_2d(xx, yy))
Plot object containing:
[0]: 2D list plot

(Source code, png)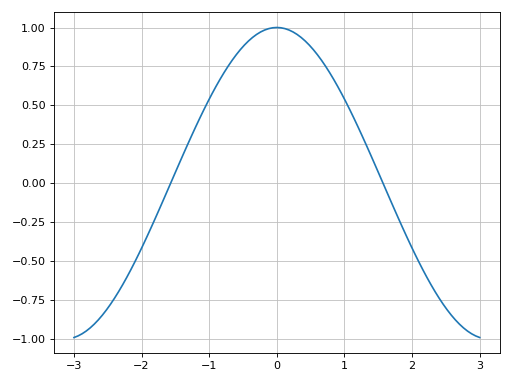

../../_images/functions_2d-39.png

Plot individual points with custom labels. Each point will be converted to a list by the algorithm:

>>> graphics(
...     list_2d(0, 0, "A", is_scatter=True),
...     list_2d(1, 1, "B", is_scatter=True),
...     list_2d(2, 0, "C", is_scatter=True),
... )
Plot object containing:
[0]: 2D list plot
[1]: 2D list plot
[2]: 2D list plot

(Source code, png)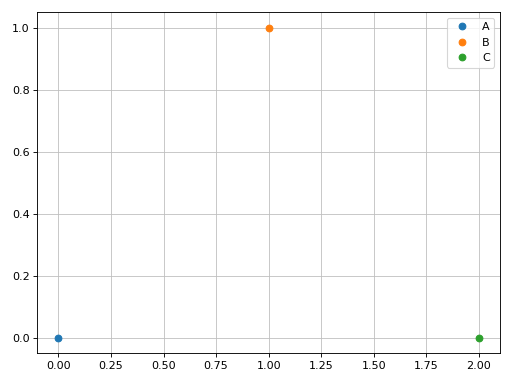

../../_images/functions_2d-40.png

Scatter plot of the coordinates of multiple functions, with custom rendering keywords:

>>> xx = [t / 70 * 6 - 3 for t in list(range(71))]
>>> yy1 = [cos(x).evalf(subs={x: t}) for t in xx]
>>> yy2 = [sin(x).evalf(subs={x: t}) for t in xx]
>>> graphics(
...     list_2d(xx, yy1, "cos", is_scatter=True),
...     list_2d(xx, yy2, "sin", {"marker": "*", "markerfacecolor": None},
...             is_scatter=True),
... )
Plot object containing:
[0]: 2D list plot
[1]: 2D list plot

(Source code, png)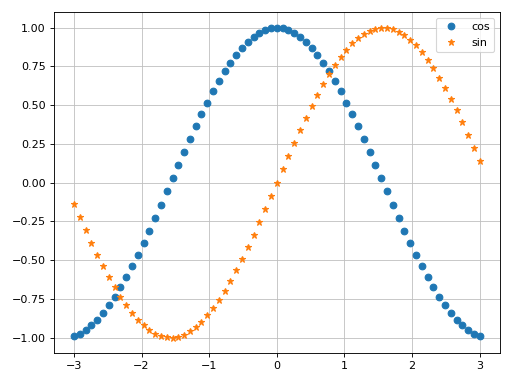

../../_images/functions_2d-41.png

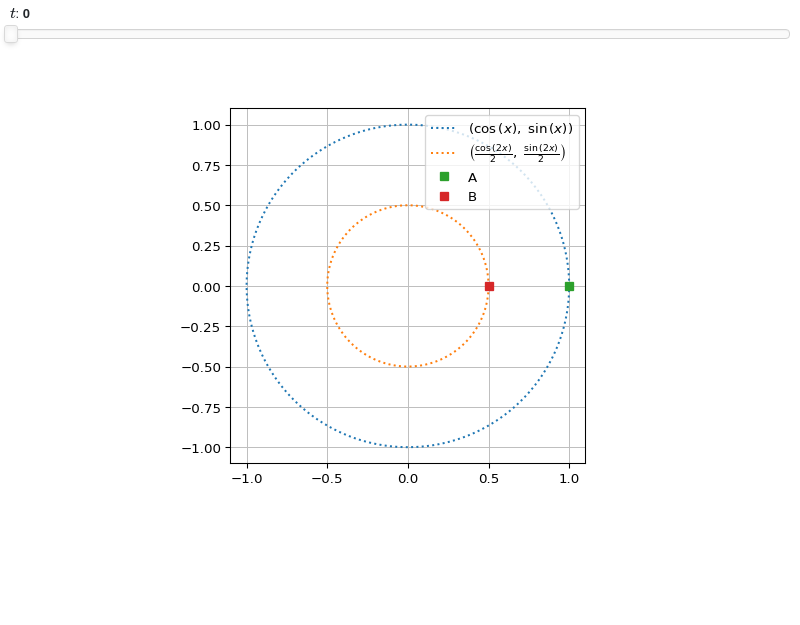
Interactive-widget plot. Refer to the interactive sub-module documentation to learn more about the params dictionary.

from sympy import *
from spb import *
x, t = symbols("x, t")
params = {t: (0, 0, 2*pi)}
graphics(
    line_parametric_2d(
        cos(x), sin(x), (x, 0, 2*pi), rendering_kw={"linestyle": ":"},
        use_cm=False),
    line_parametric_2d(
        cos(2 * x) / 2, sin(2 * x) / 2, (x, 0, pi),
        rendering_kw={"linestyle": ":"}, use_cm=False),
    list_2d(
        cos(t), sin(t), "A",
        rendering_kw={"marker": "s", "markerfacecolor": None},
        params=params, is_scatter=True),
    list_2d(
        cos(2 * t) / 2, sin(2 * t) / 2, "B",
        rendering_kw={"marker": "s", "markerfacecolor": None},
        params=params, is_scatter=True),
    aspect="equal"
)

(Source code, small.png)

../../_images/functions_2d-42.small.png
spb.graphics.functions_2d.geometry(geom, label=None, rendering_kw=None, fill=True, **kwargs)[source]

Plot entities from the sympy.geometry module.

Parameters:
geomGeometryEntity

Represent the geometric entity to be plotted.

labelstr

Set the label associated to this series, which will be eventually shown on the legend or colorbar.

rendering_kwdict

A dictionary of keyword arguments to be passed to the renderers in order to further customize the appearance of the line. Here are some useful links for the supported plotting libraries:

colorbar_ticks_formattertick_formatter_multiples_of

An object of type tick_formatter_multiples_of which will be used to place tick values on the colorbar at each multiple of a specified quantity. This only works when use_cm=True.

is_filledbool

If True, the geometry will be filled, otherwise only the perimeter will be rendered. Default value: True.

is_scatterbool

If True it represent a scatter plot, otherwise a continuous line. Default value: False.

line_color

For back-compatibility with old sympy.plotting. Use rendering_kw in order to fully customize the appearance of the line/scatter.

n1int

Number of discretization points used to resolve the polar angle theta ∈ [0, 2*pi] in order to plot ellipses. It must be: 2 ≤ n1 < ∞. Default value: 1000.

paramsdict, optional

A dictionary mapping symbols to parameters. If provided, this dictionary enables the interactive-widgets plot.

When calling a plotting function, the parameter can be specified with:

  • a widget from the ipywidgets module.

  • a widget from the panel module.

  • a tuple of the form:

    (default, min, max, N, tick_format, label, spacing), which will instantiate a ipywidgets.widgets.widget_float.FloatSlider or a ipywidgets.widgets.widget_float.FloatLogSlider, depending on the spacing strategy. In particular:

    • default, min, maxfloat

      Default value, minimum value and maximum value of the slider, respectively. Must be finite numbers. The order of these 3 numbers is not important: the module will figure it out which is what.

    • Nint, optional

      Number of steps of the slider.

    • tick_formatstr or None, optional

      Provide a formatter for the tick value of the slider. Default to ".2f".

    • label: str, optional

      Custom text associated to the slider.

    • spacingstr, optional

      Specify the discretization spacing. Default to "linear", can be changed to "log".

Notes:

  1. parameters cannot be linked together (ie, one parameter cannot depend on another one).

  2. If a widget returns multiple numerical values (like panel.widgets.slider.RangeSlider or ipywidgets.widgets.widget_float.FloatRangeSlider), then a corresponding number of symbols must be provided.

Here follows a couple of examples. If imodule="panel":

import panel as pn
params = {
    a: (1, 0, 5), # slider from 0 to 5, with default value of 1
    b: pn.widgets.FloatSlider(value=1, start=0, end=5), # same slider as above
    (c, d): pn.widgets.RangeSlider(value=(-1, 1), start=-3, end=3, step=0.1)
}

Or with imodule="ipywidgets":

import ipywidgets as w
params = {
    a: (1, 0, 5), # slider from 0 to 5, with default value of 1
    b: w.FloatSlider(value=1, min=0, max=5), # same slider as above
    (c, d): w.FloatRangeSlider(value=(-1, 1), min=-3, max=3, step=0.1)
}

When instantiating a data series directly, params must be a dictionary mapping symbols to numerical values.

Let series be any data series. Then series.params returns a dictionary mapping symbols to numerical values.

range_xtuple

A 2-tuple (min, max) denoting the range of the x variable to be used when plotting objects of type Line2D. If not provided, a segment will be plotted between the 2 specified points of the line.

show_in_legendbool

Toggle the visibility of the data series on the legend. Default value: True.

txcallable

Numerical transformation function to be applied to the data on the x-axis.

tycallable

Numerical transformation function to be applied to the data on the y-axis.

Returns:
serieslist

A list containing one instance of GeometrySeries.

See also

line, spb.graphics.functions_3d.plane

Examples

>>> from sympy import (symbols, Circle, Ellipse, Polygon,
...      Curve, Segment, Point2D, Point3D, Line3D, Plane,
...      Rational, pi, Point, cos, sin)
>>> from spb import *
>>> x, y, z = symbols('x, y, z')

(Source code)

Plot a single geometry, customizing its color:

>>> graphics(
...     geometry(
...         Ellipse(Point(-3, 2), hradius=3, eccentricity=Rational(4, 5)),
...         rendering_kw={"color": "tab:orange"}),
...     grid=False, aspect="equal"
... )
Plot object containing:
[0]: 2D geometry entity: Ellipse(Point2D(-3, 2), 3, 9/5)

(Source code, png)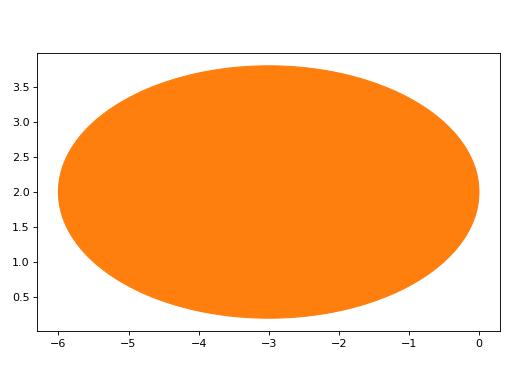

../../_images/functions_2d-44.png

Plot several numeric geometric entitiesy. By default, circles, ellipses and polygons are going to be filled. Plotting Curve objects is the same as plot_parametric.

>>> graphics(
...     geometry(Circle(Point(0, 0), 5)),
...     geometry(Ellipse(Point(-3, 2), hradius=3, eccentricity=Rational(4, 5))),
...     geometry(Polygon((4, 0), 4, n=5)),
...     geometry(Curve((cos(x), sin(x)), (x, 0, 2 * pi))),
...     geometry(Segment((-4, -6), (6, 6))),
...     geometry(Point2D(0, 0)),
...     aspect="equal", grid=False
... )
Plot object containing:
[0]: 2D geometry entity: Circle(Point2D(0, 0), 5)
[1]: 2D geometry entity: Ellipse(Point2D(-3, 2), 3, 9/5)
[2]: 2D geometry entity: RegularPolygon(Point2D(4, 0), 4, 5, 0)
[3]: parametric cartesian line: (cos(x), sin(x)) for x over (0, 2*pi)
[4]: 2D geometry entity: Segment2D(Point2D(-4, -6), Point2D(6, 6))
[5]: 2D geometry entity: Point2D(0, 0)

(Source code, png)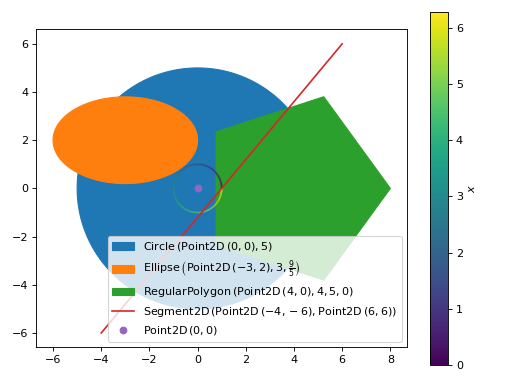

../../_images/functions_2d-45.png

Plot several numeric geometric entities defined by numbers only, turn off fill. Every entity is represented as a line.

>>> graphics(
...     geometry(Circle(Point(0, 0), 5), fill=False),
...     geometry(
...         Ellipse(Point(-3, 2), hradius=3, eccentricity=Rational(4, 5)),
...         fill=False),
...     geometry(Polygon((4, 0), 4, n=5), fill=False),
...     geometry(Curve((cos(x), sin(x)), (x, 0, 2 * pi)), fill=False),
...     geometry(Segment((-4, -6), (6, 6)), fill=False),
...     geometry(Point2D(0, 0), fill=False),
...     aspect="equal", grid=False
... )
Plot object containing:
[0]: 2D geometry entity: Circle(Point2D(0, 0), 5)
[1]: 2D geometry entity: Ellipse(Point2D(-3, 2), 3, 9/5)
[2]: 2D geometry entity: RegularPolygon(Point2D(4, 0), 4, 5, 0)
[3]: parametric cartesian line: (cos(x), sin(x)) for x over (0, 2*pi)
[4]: 2D geometry entity: Segment2D(Point2D(-4, -6), Point2D(6, 6))
[5]: 2D geometry entity: Point2D(0, 0)

(Source code, png)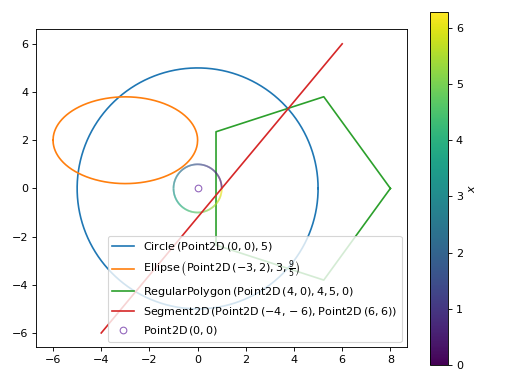

../../_images/functions_2d-46.png

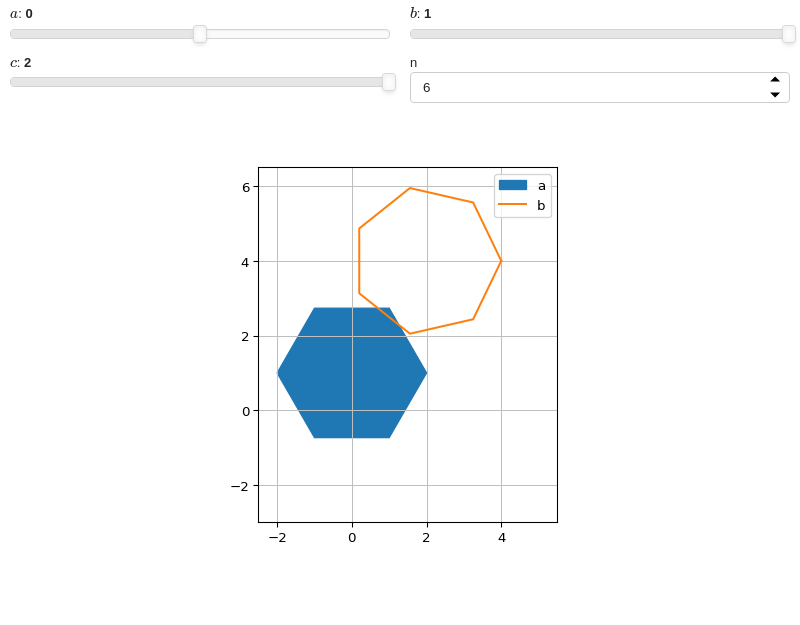
Plot 3D geometric entities. Instances of Plane must be plotted with implicit_3d or with plane (with the necessary ranges).

from sympy import *
from spb import *
x, y, z = symbols("x, y, z")
graphics(
     geometry(
         Point3D(0, 0, 0), label="center",
         rendering_kw={"point_size": 1}),
     geometry(Line3D(Point3D(-2, -3, -4), Point3D(2, 3, 4)), "line"),
     plane(
         Plane((0, 0, 0), (1, 1, 1)),
         (x, -5, 5), (y, -4, 4), (z, -10, 10)),
     backend=KB
 )

(Source code, small.png)

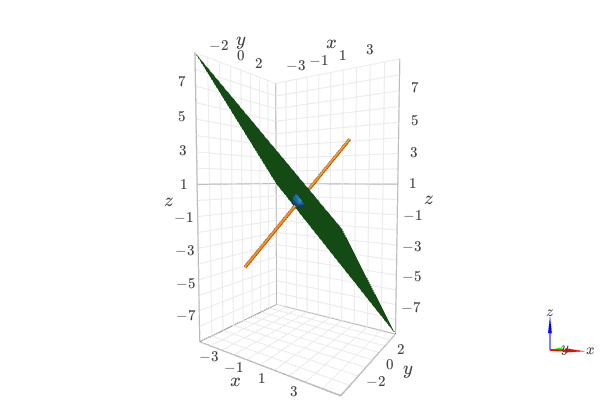
../../_images/functions_2d-47.small.png

Interactive-widget plot. Refer to the interactive sub-module documentation to learn more about the params dictionary.

from sympy import *
from spb import *
import panel as pn
a, b, c, d = symbols("a, b, c, d")
params = {
    a: (0, -1, 1),
    b: (1, -1, 1),
    c: (2, 1, 2),
    d: pn.widgets.IntInput(value=6, start=3, end=8, name="n")
}
graphics(
    geometry(Polygon((a, b), c, n=d), "a", params=params),
    geometry(
        Polygon((a + 2, b + 3), c, n=d + 1), "b",
        params=params, fill=False),
    aspect="equal",
    xlim=(-2.5, 5.5), ylim=(-3, 6.5), imodule="panel")

(Source code, small.png)

../../_images/functions_2d-48.small.png
spb.graphics.functions_2d.hline(y, label=None, rendering_kw=None, show_in_legend=True, **kwargs)[source]

Create an horizontal line at a given location in a 2D space.

Parameters:
yExpr

The y-coordinate where to draw the horizontal line.

labelstr

Set the label associated to this series, which will be eventually shown on the legend or colorbar.

rendering_kwdict

Keyword arguments to be passed to the renderers of the selected plotting library in order to further customize the appearance of this data series.

show_in_legendbool

Toggle the visibility of the data series on the legend. Default value: True.

paramsdict, optional

A dictionary mapping symbols to parameters. If provided, this dictionary enables the interactive-widgets plot.

When calling a plotting function, the parameter can be specified with:

  • a widget from the ipywidgets module.

  • a widget from the panel module.

  • a tuple of the form:

    (default, min, max, N, tick_format, label, spacing), which will instantiate a ipywidgets.widgets.widget_float.FloatSlider or a ipywidgets.widgets.widget_float.FloatLogSlider, depending on the spacing strategy. In particular:

    • default, min, maxfloat

      Default value, minimum value and maximum value of the slider, respectively. Must be finite numbers. The order of these 3 numbers is not important: the module will figure it out which is what.

    • Nint, optional

      Number of steps of the slider.

    • tick_formatstr or None, optional

      Provide a formatter for the tick value of the slider. Default to ".2f".

    • label: str, optional

      Custom text associated to the slider.

    • spacingstr, optional

      Specify the discretization spacing. Default to "linear", can be changed to "log".

Notes:

  1. parameters cannot be linked together (ie, one parameter cannot depend on another one).

  2. If a widget returns multiple numerical values (like panel.widgets.slider.RangeSlider or ipywidgets.widgets.widget_float.FloatRangeSlider), then a corresponding number of symbols must be provided.

Here follows a couple of examples. If imodule="panel":

import panel as pn
params = {
    a: (1, 0, 5), # slider from 0 to 5, with default value of 1
    b: pn.widgets.FloatSlider(value=1, start=0, end=5), # same slider as above
    (c, d): pn.widgets.RangeSlider(value=(-1, 1), start=-3, end=3, step=0.1)
}

Or with imodule="ipywidgets":

import ipywidgets as w
params = {
    a: (1, 0, 5), # slider from 0 to 5, with default value of 1
    b: w.FloatSlider(value=1, min=0, max=5), # same slider as above
    (c, d): w.FloatRangeSlider(value=(-1, 1), min=-3, max=3, step=0.1)
}

When instantiating a data series directly, params must be a dictionary mapping symbols to numerical values.

Let series be any data series. Then series.params returns a dictionary mapping symbols to numerical values.

Returns:
A list containing one instance of HVLineSeries.

See also

line

Examples

>>> from sympy import *
>>> from spb import *
>>> x = symbols("x")
>>> graphics(
...     line(cos(x), (x, -pi, pi)),
...     hline(
...         0.5, rendering_kw={"linestyle": ":"},
...         show_in_legend=False),
...     grid=False
... )
Plot object containing:
[0]: cartesian line: cos(x) for x over (-pi, pi)
[1]: horizontal line at y = 0.500000000000000

(Source code, png)

../../_images/functions_2d-49.png

Interactive widget plot:

from sympy import *
from spb import *
x, u, v, w = symbols("x u v w")
params = {
    u: (1, 0, 2),
    v: (1, 0, 2),
    w: (0.5, -1, 1)
}
graphics(
    line(u * cos(v * x), (x, -pi, pi), params=params),
    hline(
        w, rendering_kw={"linestyle": ":"},
        show_in_legend=False, params=params),
    grid=False, ylim=(-2, 2)
)

(Source code, small.png)

../../_images/functions_2d-50.small.png
spb.graphics.functions_2d.vline(x, label=None, rendering_kw=None, show_in_legend=True, **kwargs)[source]

Create an vertical line at a given location in a 2D space.

Parameters:
xExpr

The x-coordinate where to draw the vertical line.

labelstr

Set the label associated to this series, which will be eventually shown on the legend or colorbar.

rendering_kwdict

Keyword arguments to be passed to the renderers of the selected plotting library in order to further customize the appearance of this data series.

show_in_legendbool

Toggle the visibility of the data series on the legend. Default value: True.

paramsdict, optional

A dictionary mapping symbols to parameters. If provided, this dictionary enables the interactive-widgets plot.

When calling a plotting function, the parameter can be specified with:

  • a widget from the ipywidgets module.

  • a widget from the panel module.

  • a tuple of the form:

    (default, min, max, N, tick_format, label, spacing), which will instantiate a ipywidgets.widgets.widget_float.FloatSlider or a ipywidgets.widgets.widget_float.FloatLogSlider, depending on the spacing strategy. In particular:

    • default, min, maxfloat

      Default value, minimum value and maximum value of the slider, respectively. Must be finite numbers. The order of these 3 numbers is not important: the module will figure it out which is what.

    • Nint, optional

      Number of steps of the slider.

    • tick_formatstr or None, optional

      Provide a formatter for the tick value of the slider. Default to ".2f".

    • label: str, optional

      Custom text associated to the slider.

    • spacingstr, optional

      Specify the discretization spacing. Default to "linear", can be changed to "log".

Notes:

  1. parameters cannot be linked together (ie, one parameter cannot depend on another one).

  2. If a widget returns multiple numerical values (like panel.widgets.slider.RangeSlider or ipywidgets.widgets.widget_float.FloatRangeSlider), then a corresponding number of symbols must be provided.

Here follows a couple of examples. If imodule="panel":

import panel as pn
params = {
    a: (1, 0, 5), # slider from 0 to 5, with default value of 1
    b: pn.widgets.FloatSlider(value=1, start=0, end=5), # same slider as above
    (c, d): pn.widgets.RangeSlider(value=(-1, 1), start=-3, end=3, step=0.1)
}

Or with imodule="ipywidgets":

import ipywidgets as w
params = {
    a: (1, 0, 5), # slider from 0 to 5, with default value of 1
    b: w.FloatSlider(value=1, min=0, max=5), # same slider as above
    (c, d): w.FloatRangeSlider(value=(-1, 1), min=-3, max=3, step=0.1)
}

When instantiating a data series directly, params must be a dictionary mapping symbols to numerical values.

Let series be any data series. Then series.params returns a dictionary mapping symbols to numerical values.

Returns:
A list containing one instance of HVLineSeries.

See also

line

Examples

>>> from sympy import *
>>> from spb import *
>>> x = symbols("x")
>>> graphics(
...     line(cos(x), (x, -pi, pi)),
...     vline(1, rendering_kw={"linestyle": ":"}, show_in_legend=False),
...     vline(-1, rendering_kw={"linestyle": ":"}, show_in_legend=False),
...     grid=False
... )
Plot object containing:
[0]: cartesian line: cos(x) for x over (-pi, pi)
[1]: vertical line at x = 1
[2]: vertical line at x = -1

(Source code, png)

../../_images/functions_2d-51.png

Interactive widget plot:

from sympy import *
from spb import *
x, u, v, w = symbols("x u v w")
params = {
    u: (1, 0, 2),
    v: (1, 0, 2),
    w: (1, -pi, pi)
}
graphics(
    line(u * cos(v * x), (x, -pi, pi), params=params),
    vline(
        w, rendering_kw={"linestyle": ":"},
        show_in_legend=False, params=params),
    grid=False, ylim=(-2, 2)
)

(Source code, small.png)

../../_images/functions_2d-52.small.png