Vectors

NOTE: For technical reasons, all interactive-widgets plots in this documentation are created using Holoviz’s Panel. Often, they will ran just fine with ipywidgets too. However, if a specific example uses the param library, or widgets from the panel module, then users will have to modify the params dictionary in order to make it work with ipywidgets. Refer to Interactive module for more information.

spb.graphics.vectors.arrow_2d(start, direction, label=None, rendering_kw=None, show_in_legend=True, **kwargs)[source]

Draw an arrow in a 2D space.

Parameters:

start(x, y): Coordinates of the start position.
direction(u, v): Componenents of the direction vector.
labelstr, optional: The label to be shown in the legend. If not provided, the string representation of expr will be used.
rendering_kwdict, optional: A dictionary of keywords/values which is passed to the backend’s function to customize the appearance of lines. Refer to the plotting library (backend) manual for more informations.
show_in_legendbool: If True, add a legend entry for the expression being plotted. This option is useful to hide a particular expression when combining together multiple plots. Default to True.

Returns:

A list containing one instance of Arrow2DSeries.

See also

vector_field_2d

Examples

>>> from spb import *
>>> graphics(
...     arrow_2d((0, 0), (1, 1)),
...     arrow_2d((0, 0), (-1, 1)),
...     grid=False, aspect="equal"
... )
Plot object containing:
[0]: 2D arrow from (0.0, 0.0) to (1.0, 1.0)
[1]: 2D arrow from (0.0, 0.0) to (-1.0, 1.0)

(Source code, png)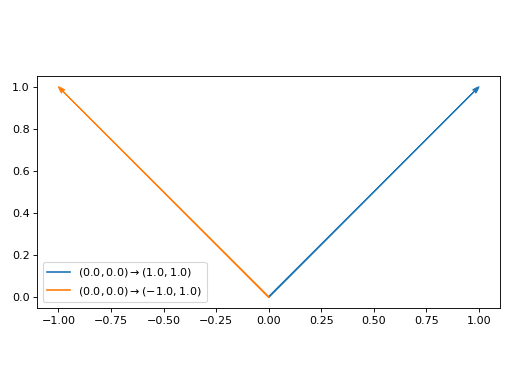

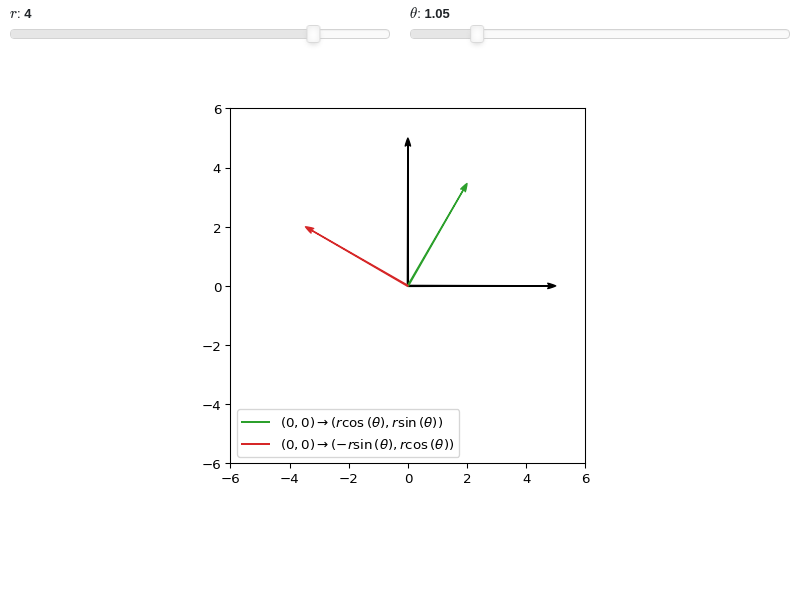
Interactive-widget plot of arrows. Refer to the interactive sub-module documentation to learn more about the params dictionary.

from sympy import *
from spb import *
r, theta = symbols("r, theta")
params = {
    r: (4, 0, 5),
    theta: (pi/3, 0, 2*pi),
}
graphics(
    arrow_2d(
        (0, 0), (5, 0), show_in_legend=False,
        rendering_kw={"color": "k"}),
    arrow_2d(
        (0, 0), (0, 5), show_in_legend=False,
        rendering_kw={"color": "k"}),
    arrow_2d(
        (0, 0), (r * cos(theta), r * sin(theta)),
        params=params),
    arrow_2d(
        (0, 0), (r * cos(theta + pi/2), r * sin(theta + pi/2)),
        params=params),
    xlim=(-6, 6), ylim=(-6, 6), aspect="equal",
    grid=False
)

(Source code, small.png)

spb.graphics.vectors.arrow_3d(start, direction, label=None, rendering_kw=None, show_in_legend=True, **kwargs)[source]

Draw an arrow in a 2D space.

Parameters:

start(x, y, z): Coordinates of the start position.
direction(u, v, w): Componenents of the direction vector.
labelstr, optional: The label to be shown in the legend. If not provided, the string representation of expr will be used.
rendering_kwdict, optional: A dictionary of keywords/values which is passed to the backend’s function to customize the appearance of lines. Refer to the plotting library (backend) manual for more informations.
show_in_legendbool: If True, add a legend entry for the expression being plotted. This option is useful to hide a particular expression when combining together multiple plots. Default to True.

Returns:

A list containing one instance of Arrow3DSeries.

See also

arrow_2d, vector_field_3d

Examples

>>> from spb import *
>>> graphics(
...     arrow_3d((0, 0, 0), (1, 0, 0)),
...     arrow_3d((0, 0, 0), (0, 1, 0)),
...     arrow_3d((0, 0, 0), (0, 0, 1), show_in_legend=False,
...              rendering_kw={
...                  "mutation_scale": 20,
...                  "arrowstyle": "-|>",
...                  "linestyle": 'dashed',
...              }),
...     xlabel="x", ylabel="y", zlabel="z")
Plot object containing:
[0]: 3D arrow from (0.0, 0.0, 0.0) to (1.0, 0.0, 0.0)
[1]: 3D arrow from (0.0, 0.0, 0.0) to (0.0, 1.0, 0.0)
[2]: 3D arrow from (0.0, 0.0, 0.0) to (0.0, 0.0, 1.0)

(Source code, png)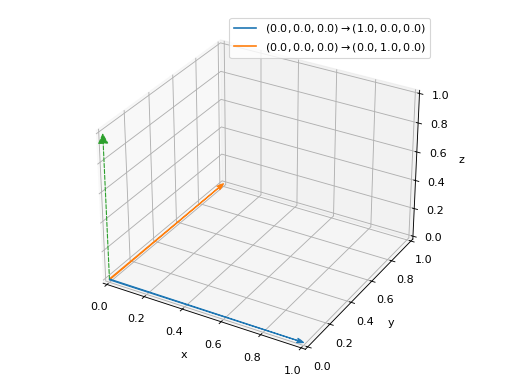

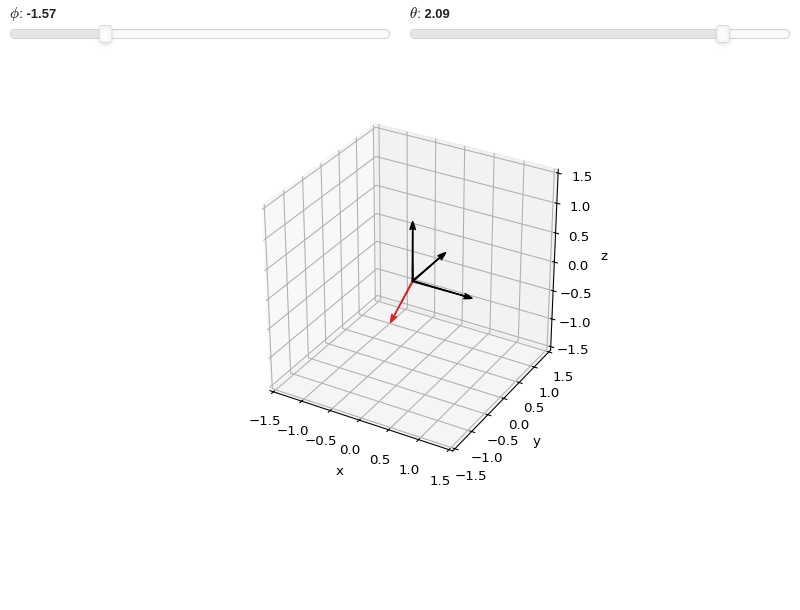
Interactive-widget plot of arrows. Refer to the interactive sub-module documentation to learn more about the params dictionary.

from sympy import *
from spb import *
phi, theta = symbols("phi, theta")
r = 0.75
params = {
    phi: (-pi/2, -pi, pi),
    theta: (2*pi/3, -pi, pi),
}
graphics(
    arrow_3d((0, 0, 0), (1, 0, 0), rendering_kw={"color": "k"},
        show_in_legend=False),
    arrow_3d((0, 0, 0), (0, 1, 0), rendering_kw={"color": "k"},
        show_in_legend=False),
    arrow_3d((0, 0, 0), (0, 0, 1), rendering_kw={"color": "k"},
        show_in_legend=False),
    arrow_3d(
        (0, 0, 0),
        (r*sin(theta)*cos(phi), r*sin(theta)*sin(phi), r*cos(theta)),
        params=params),
    xlabel="x", ylabel="y", zlabel="z",
    xlim=(-1.5, 1.5), ylim=(-1.5, 1.5), zlim=(-1.5, 1.5), aspect="equal"
)

(Source code, small.png)

spb.graphics.vectors.vector_field_2d(expr1, expr2=None, range1=None, range2=None, label=None, quiver_kw=None, stream_kw=None, contour_kw=None, **kwargs)[source]

Plot a 2D vector field.

Parameters:

expr1, expr2Vector, Expr or callable

The components of the vector field. It can be a:

A vector from the sympy.vector module or from the sympy.physics.mechanics module. In this case, only expr1 is set.
Two symbolic expressions, one for each component.
Two numerical functions of 2 variables.

range1, range23-element tuples

Denotes the range of the variables. For example (x, -5, 5).

labelstr, optional

The name of the vector field to be eventually shown on the legend or colorbar. If none is provided, the string representation of the vector will be used.

colorbarboolean, optional

Show/hide the colorbar. Default to True (colorbar is visible).

color_funccallable, optional

Define the quiver/streamlines color mapping when use_cm=True. It can either be:

A numerical function supporting vectorization. The arity must be: f(x, y, u, v). Further, scalar=False must be set in order to hide the contour plot so that a colormap is applied to quivers/streamlines.
A symbolic expression having at most as many free symbols as expr1/expr2. This only works for quivers plot.
None: the default value, which will map colors according to the magnitude of the vector field.

contour_kwdict, optional

A dictionary of keywords/values which is passed to the backend contour function to customize the appearance. Refer to the plotting library (backend) manual for more informations.

n, n1, n2int, optional

Number of discretization points for the quivers or streamlines in the x/y-direction, respectively. Default to 25. n is a shortcut to set the same number of discretization points on both directions.

ncint, optional

Number of discretization points for the scalar contour plot. Default to 100.

normalizebool, optional

Default to False. If True, the vector field will be normalized, resulting in quivers having the same length. If use_cm=True, the backend will color the quivers by the (pre-normalized) vector field’s magnitude. Note: only quivers will be affected by this option.

paramsdict, optional

A dictionary mapping symbols to parameters. This keyword argument enables the interactive-widgets plot. Learn more by reading the documentation of the interactive sub-module.

quiver_kwdict, optional

A dictionary of keywords/values which is passed to the backend quivers- plotting function to customize the appearance. Refer to the plotting library (backend) manual for more informations.

scalarboolean, Expr, None or list/tuple of 2 elements, optional

Represents the scalar field to be plotted in the background of a 2D vector field plot. It can be:

True: plot the magnitude of the vector field. Only works when a single vector field is plotted.
False/None: do not plot any scalar field.
Expr: a symbolic expression representing the scalar field.
a numerical function of 2 variables supporting vectorization.
list/tuple: [scalar_expr, label], where the label will be shown on the colorbar. scalar_expr can be a symbolic expression or a numerical function of 2 variables supporting vectorization.

Default to True.

show_in_legendbool

If True, add a legend entry for the expression being plotted. This option is useful to hide a particular expression when combining together multiple plots. Default to True.

streamlinesboolean, optional

Whether to plot the vector field using streamlines (True) or quivers (False). Default to False.

stream_kwdict, optional

A dictionary of keywords/values which is passed to the backend streamlines-plotting function to customize the appearance. Refer to the Notes section to learn more.

Returns:

serieslist: A list containing one instance of ContourSeries (if scalar is set) and one instance of Vector2DSeries.

See also

vector_field_3d

Examples

>>> from sympy import symbols, sin, cos, Plane, Matrix, sqrt, latex
>>> from spb import *
>>> x, y, z = symbols('x, y, z')

(Source code)

Quivers plot of a 2D vector field with a contour plot in background representing the vector’s magnitude (a scalar field).

>>> graphics(
...     vector_field_2d(sin(x - y), cos(x + y), (x, -3, 3), (y, -3, 3),
...         quiver_kw=dict(color="black", scale=30, headwidth=5),
...         contour_kw={"cmap": "Blues_r", "levels": 15}),
...     grid=False, xlabel="x", ylabel="y")
Plot object containing:
[0]: contour: sqrt(sin(x - y)**2 + cos(x + y)**2) for x over (-3.0, 3.0) and y over (-3.0, 3.0)
[1]: 2D vector series: [sin(x - y), cos(x + y)] over (x, -3.0, 3.0), (y, -3.0, 3.0)

(Source code, png)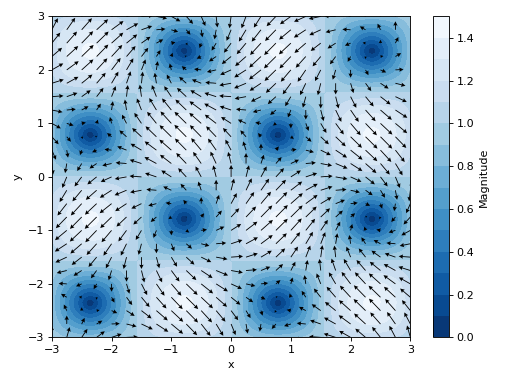

Quivers plot of a 2D vector field with no background scalar field, a custom label and normalized quiver lengths:

>>> graphics(
...     vector_field_2d(sin(x - y), cos(x + y), (x, -3, 3), (y, -3, 3),
...         label="Magnitude of $%s$" % latex([-sin(y), cos(x)]),
...         scalar=False, normalize=True,
...         quiver_kw={
...             "scale": 35, "headwidth": 4, "cmap": "gray",
...             "clim": [0, 1.6]}),
...     grid=False, xlabel="x", ylabel="y")
Plot object containing:
[0]: 2D vector series: [sin(x - y), cos(x + y)] over (x, -3.0, 3.0), (y, -3.0, 3.0)

(Source code, png)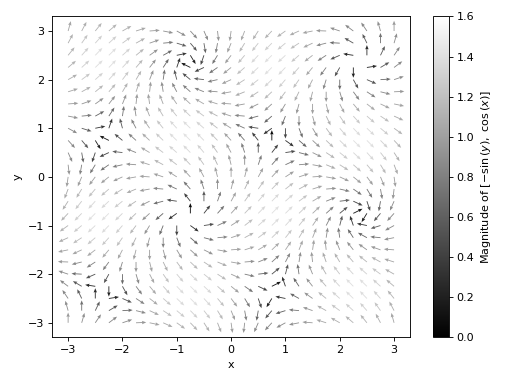

Streamlines plot of a 2D vector field with no background scalar field, and a custom label:

>>> graphics(
...     vector_field_2d(sin(x - y), cos(x + y), (x, -3, 3), (y, -3, 3),
...         streamlines=True, scalar=None,
...         stream_kw={"density": 1.5},
...         label="Magnitude of %s" % str([sin(x - y), cos(x + y)])),
...     xlabel="x", ylabel="y", grid=False)
Plot object containing:
[0]: 2D vector series: [sin(x - y), cos(x + y)] over (x, -3.0, 3.0), (y, -3.0, 3.0)

(Source code, png)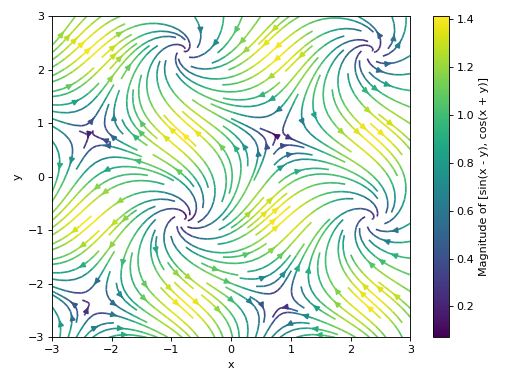

Plot multiple 2D vectors fields, setting a background scalar field to be the magnitude of the first vector. Also, apply custom rendering options to all data series.

>>> scalar_expr = sqrt((-sin(y))**2 + cos(x)**2)
>>> graphics(
...     vector_field_2d(-sin(y), cos(x), (x, -5, 5), (y, -3, 3), n=20,
...         scalar=[scalar_expr, "$%s$" % latex(scalar_expr)],
...         contour_kw={"cmap": "summer"},
...         quiver_kw={"color": "k"}),
...     vector_field_2d(2 * y, x, (x, -5, 5), (y, -3, 3), n=20,
...         scalar=False, quiver_kw={"color": "r"}, use_cm=False),
...     aspect="equal", grid=False, xlabel="x", ylabel="y")
Plot object containing:
[0]: contour: sqrt(sin(y)**2 + cos(x)**2) for x over (-5.0, 5.0) and y over (-3.0, 3.0)
[1]: 2D vector series: [-sin(y), cos(x)] over (x, -5.0, 5.0), (y, -3.0, 3.0)
[2]: 2D vector series: [2*y, x] over (x, -5.0, 5.0), (y, -3.0, 3.0)

(Source code, png)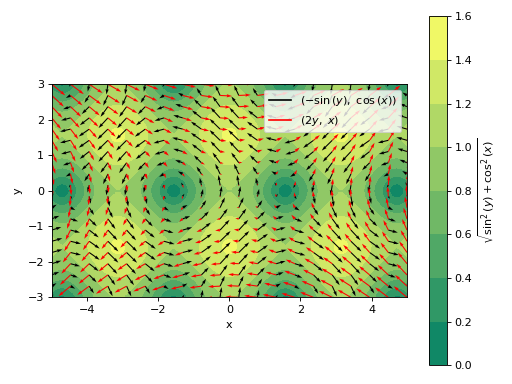

Plotting a the streamlines of a 2D vector field defined with numerical functions instead of symbolic expressions:

>>> import numpy as np
>>> f = lambda x, y: np.sin(2 * x + 2 * y)
>>> fx = lambda x, y: np.cos(f(x, y))
>>> fy = lambda x, y: np.sin(f(x, y))
>>> graphics(
...     vector_field_2d(fx, fy, ("x", -1, 1), ("y", -1, 1),
...         streamlines=True, scalar=False, use_cm=False),
...     aspect="equal", xlabel="x", ylabel="y", grid=False
... )  

(Source code, png)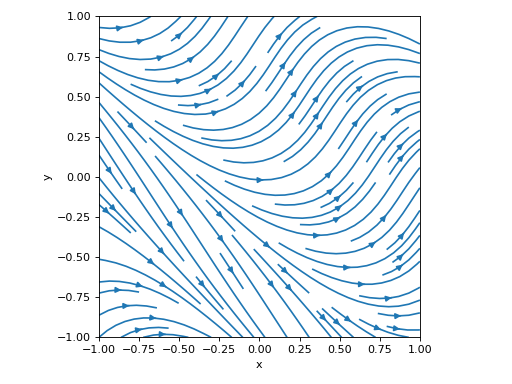

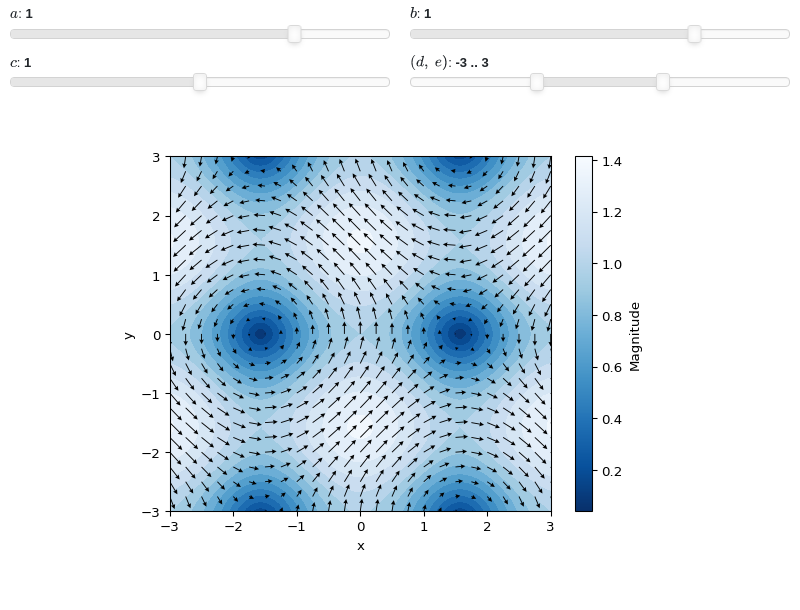
Interactive-widget 2D vector plot. Refer to the interactive sub-module documentation to learn more about the params dictionary. This plot illustrates:

customizing the appearance of quivers and countour.
the use of prange (parametric plotting range).
the use of the params dictionary to specify sliders in their basic form: (default, min, max).
the use of panel.widgets.slider.RangeSlider, which is a 2-values widget.

from sympy import *
from spb import *
import panel as pn
x, y, a, b, c, d, e = symbols("x, y, a, b, c, d, e")
v = [-sin(a * y), cos(b * x)]
graphics(
    vector_field_2d(-sin(a * y), cos(b * x),
        prange(x, -3*c, 3*c), prange(y, d, e),
        params={
            a: (1, -2, 2), b: (1, -2, 2),
            c: (1, 0, 2),
            (d, e): pn.widgets.RangeSlider(
                value=(-3, 3), start=-9, end=9, step=0.1)
        },
        quiver_kw=dict(color="black", scale=30, headwidth=5),
        contour_kw={"cmap": "Blues_r", "levels": 15}
    ),
    grid=False, xlabel="x", ylabel="y")

(Source code, small.png)

spb.graphics.vectors.vector_field_3d(expr1, expr2=None, expr3=None, range1=None, range2=None, range3=None, label=None, quiver_kw=None, stream_kw=None, **kwargs)[source]

Plot a 3D vector field.

Parameters:

expr1, expr2, expr3Vector, Expr or callable

The components of the vector field. It can be a:

A vector from the sympy.vector module or from the sympy.physics.mechanics module. In this case, only expr1 is set.
Three symbolic expressions, one for each component.
Three numerical functions of 3 variables.

range1, range2, range33-element tuples

Denotes the range of the variables. For example (x, -5, 5).

labelstr, optional

The name of the vector field to be eventually shown on the legend or colorbar. If none is provided, the string representation of the vector will be used.

colorbarboolean, optional

Show/hide the colorbar. Default to True (colorbar is visible).

color_funccallable, optional

Define the quiver/streamlines color mapping when use_cm=True. It can either be:

A numerical function supporting vectorization. The arity must be f(x, y, z, u, v, w).
A symbolic expression having at most as many free symbols as expr1/expr2/expr3. This only works for quivers plot.
None: the default value, which will map colors according to the magnitude of the vector.

contour_kwdict, optional

A dictionary of keywords/values which is passed to the backend contour function to customize the appearance. Refer to the plotting library (backend) manual for more informations.

n, n1, n2int, optional

Number of discretization points for the quivers or streamlines in the x/y/z-direction, respectively. Default to 25. n is a shortcut to set the same number of discretization points on all directions.

normalizebool, optional

Default to False. If True, the vector field will be normalized, resulting in quivers having the same length. If use_cm=True, the backend will color the quivers by the (pre-normalized) vector field’s magnitude. Note: only quivers will be affected by this option.

paramsdict, optional

A dictionary mapping symbols to parameters. This keyword argument enables the interactive-widgets plot. Learn more by reading the documentation of the interactive sub-module.

quiver_kwdict, optional

A dictionary of keywords/values which is passed to the backend quivers- plotting function to customize the appearance. Refer to the plotting library (backend) manual for more informations.

slicePlane, list, Expr, optional

Plot the 3D vector field over the provided slice. It can be:

a Plane object from sympy.geometry module.
a list of planes.
an instance of SurfaceOver2DRangeSeries or ParametricSurfaceSeries.
a symbolic expression representing a surface of two variables.

The number of discretization points will be n1, n2, n3. Note that:

only quivers plots are supported with slices. Streamlines plots are unaffected.
n3 will only be used with planes parallel to xz or yz.
n1, n2, n3 doesn’t affect the slice if it is an instance of SurfaceOver2DRangeSeries or ParametricSurfaceSeries.

streamlinesboolean, optional

Whether to plot the vector field using streamlines (True) or quivers (False). Default to False.

stream_kwdict, optional

A dictionary of keywords/values which is passed to the backend streamlines-plotting function to customize the appearance.

By default, the streamlines will start at the boundaries of the domain where the vectors are pointed inward. Depending on the vector field, this may results in too tight streamlines. Use the starts keyword argument to control the generation of streamlines:

starts=None: the default aforementioned behaviour.
starts=dict(x=x_list, y=y_list, z=z_list): specify the starting points of the streamlines.
starts=True: randomly create starting points inside the domain. In this setup we can set the number of starting point with npoints (default value to 200).

If 3D streamlines appears to be cut short inside the specified domain, try to increase max_prop (default value to 5000).

Returns:

serieslist: If slice is not set, the function returns a list containing one instance of Vector3DSeries. Conversely, it returns a list containing instances of SliceVector3DSeries.

See also

vector_field_2d

Examples

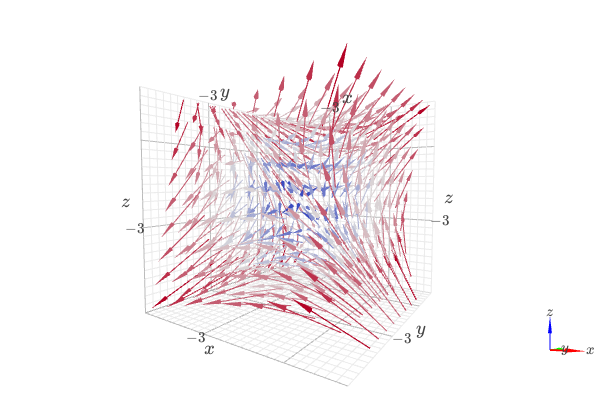
3D vector field.

from sympy import *
from spb import *
var("x:z")
graphics(
    vector_field_3d(z, y, x, (x, -10, 10), (y, -10, 10), (z, -10, 10),
        n=8, quiver_kw={"scale": 0.5, "line_width": 0.1, "head_size": 10}),
    backend=KB, xlabel="x", ylabel="y", zlabel="z")

(Source code, small.png)

3D vector field with 3 orthogonal slice planes.

from sympy import *
from spb import *
var("x:z")
graphics(
    vector_field_3d(z, y, x, (x, -10, 10), (y, -10, 10), (z, -10, 10),
        n=8, use_cm=False,
        quiver_kw={"scale": 0.25, "line_width": 0.1, "head_size": 10},
        slice=[
            Plane((-10, 0, 0), (1, 0, 0)),
            Plane((0, 10, 0), (0, 2, 0)),
            Plane((0, 0, -10), (0, 0, 1))]
    ),
    backend=KB, grid=False, xlabel="x", ylabel="y", zlabel="z",)

(Source code, small.png)

3D vector streamlines starting at a 300 random points:

from sympy import *
from spb import *
import k3d
var("x:z")
graphics(
    vector_field_3d(z, -x, y, (x, -3, 3), (y, -3, 3), (z, -3, 3),
        n=40, streamlines=True,
        stream_kw=dict(
            starts=True,
            npoints=400,
            width=0.025,
            color_map=k3d.colormaps.matplotlib_color_maps.viridis
        )
    ),
    backend=KB, xlabel="x", ylabel="y", zlabel="z")

(Source code, small.png)

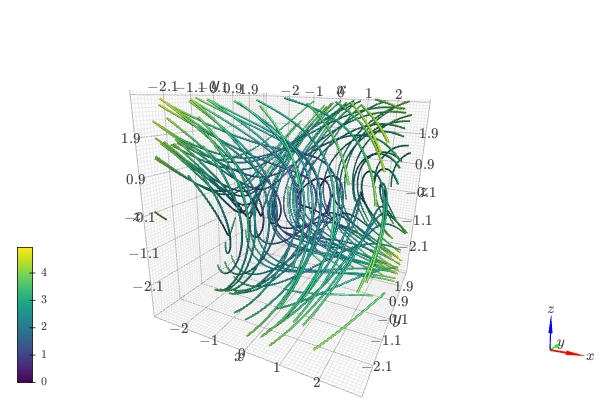
3D vector streamlines starting at the XY plane. Note that the number of discretization points of the plane controls the numbers of streamlines.

from sympy import *
from spb import *
import k3d
var("x:z")
u = -y - z
v = x + y / 5
w = S(1) / 5 + (x - S(5) / 2) * z
s = 10 # length of the cubic discretization volume
# create an XY plane with n discretization points along each direction
n = 8
p = plane(
    Plane((0, 0, 0), (0, 0, 1)), (x, -s, s), (y, -s, s), (z, -s, s),
    n1=n, n2=n)[0]
xx, yy, zz = p.get_data()
graphics(
    vector_field_3d(
        u, v, w, (x, -s, s), (y, -s, s), (z, -s, s),
        n=40, streamlines=True,
        stream_kw=dict(
            starts=dict(x=xx, y=yy, z=zz),
            width=0.025,
            color_map=k3d.colormaps.matplotlib_color_maps.plasma
        )),
    title=r"Rössler \, attractor", xlabel="x", ylabel="y", zlabel="z",
    backend=KB, grid=False)

(Source code, small.png)

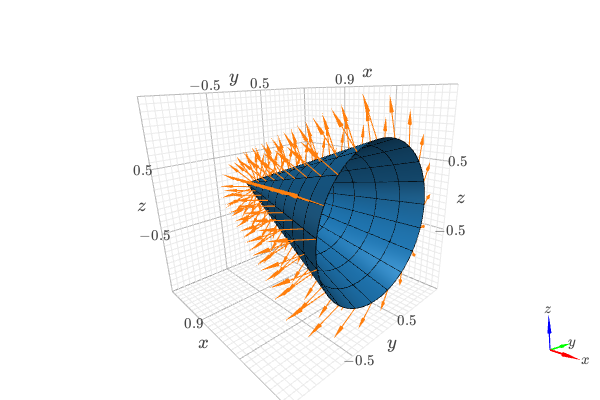
Visually verify the normal vector to a circular cone surface. The following steps are executed:

compute the normal vector to a circular cone surface. This will be the vector field to be plotted.
plot the cone surface for visualization purposes (use high number of discretization points).
plot the cone surface that will be used to slice the vector field (use a low number of discretization points). The data series associated to this plot will be used in the slice keyword argument in the next step.
plot the sliced vector field.
combine the plots of step 4 and 2 to get a nice visualization.

from sympy import tan, cos, sin, pi, symbols
from spb import *
from sympy.vector import CoordSys3D, gradient

u, v = symbols("u, v")
N = CoordSys3D("N")
i, j, k = N.base_vectors()
xn, yn, zn = N.base_scalars()

t = 0.35    # half-cone angle in radians
expr = -xn**2 * tan(t)**2 + yn**2 + zn**2    # cone surface equation
g = gradient(expr)
n = g / g.magnitude()    # unit normal vector
n1, n2 = 10, 20 # number of discretization points for the vector field

# cone surface to discretize vector field (low numb of discret points)
cone_discr = surface_parametric(
    u / tan(t), u * cos(v), u * sin(v), (u, 0, 1), (v, 0 , 2*pi),
    n1=n1, n2=n2)[0]
graphics(
    surface_parametric(
        u / tan(t), u * cos(v), u * sin(v), (u, 0, 1), (v, 0 , 2*pi),
        rendering_kw={"opacity": 1}, wireframe=True,
        wf_n1=n1, wf_n2=n2, wf_rendering_kw={"width": 0.004}),
    vector_field_3d(
        n, range1=(xn, -5, 5), range2=(yn, -5, 5), range3=(zn, -5, 5),
        use_cm=False, slice=cone_discr,
        quiver_kw={"scale": 0.5, "pivot": "tail"}
    ),
    backend=KB)

(Source code, small.png)